Reverse常见算法

1byte->2**n bytes

  • 非对称加密：RSA ECC SM2 SM9
  • 哈希：MD5 SHA SM3
  • base58（整除）

1byte->n bytes

  • 分组：SM1 SM4 SM7
  • base16,32,64,85

1byte->1 byte

  • 替换密码
  • RC4 ZUC

base64

核心：三转四

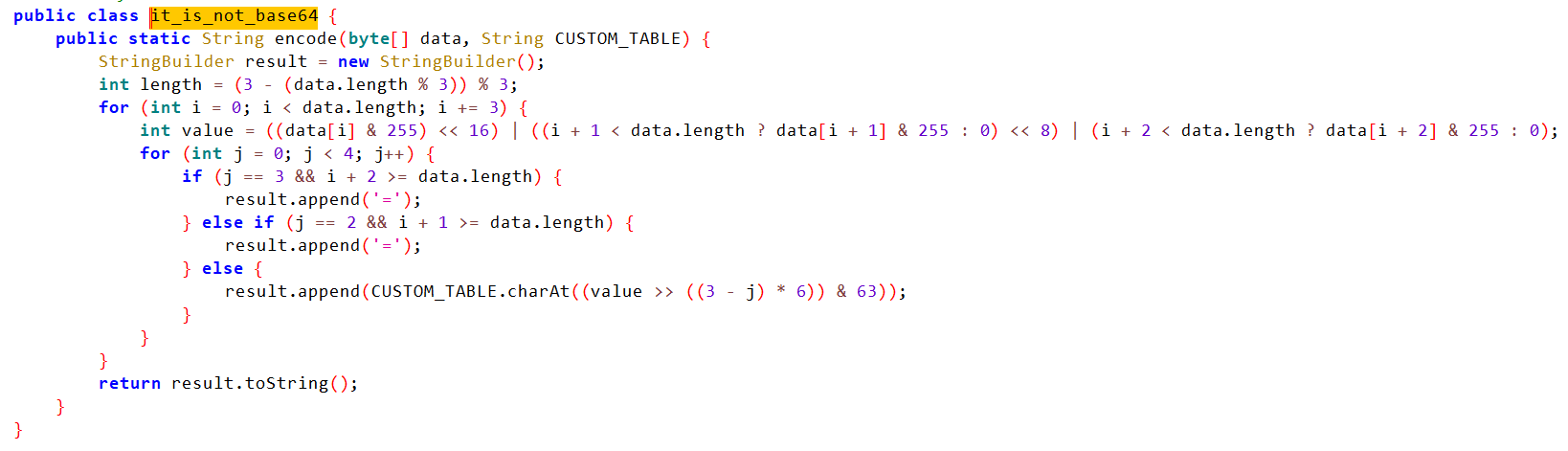
补充一下我对倒数第四行的的困惑及解释：字母和3进行与操作只保留字母的二进制最后两位，左移4相当于给低四位加0，一共是六位；后半部分直接右移4，相当于只剩4位，两数取或运算后面的数虽然只有4位，但前面可以补0，且一个数跟0进行或运算取决于它自身，所以一共是6位

有时候会是下面的形式，主要一下子没看出来，记录一下。发现>>2和&0x3f还是在的，另外一些用位操作代替了，且对字符串的长度根据%3的余数做了分类

也有这种位运算之后全是&0x3f的

%3和=告诉我下面的也是base64

RC4

1.先初始化状态向量S（用来作为密钥流生成的种子1）

2.初始密钥key（由用户输入），长度任意,如果输入长度小于256个字节，则进行循环，直到填满k,有时候k用t来表示

3.开始对状态向量S进行置换操作（用来打乱初始种子1）

KSA

4.生成密钥

PGRA

rc4也可以&255(0xff)

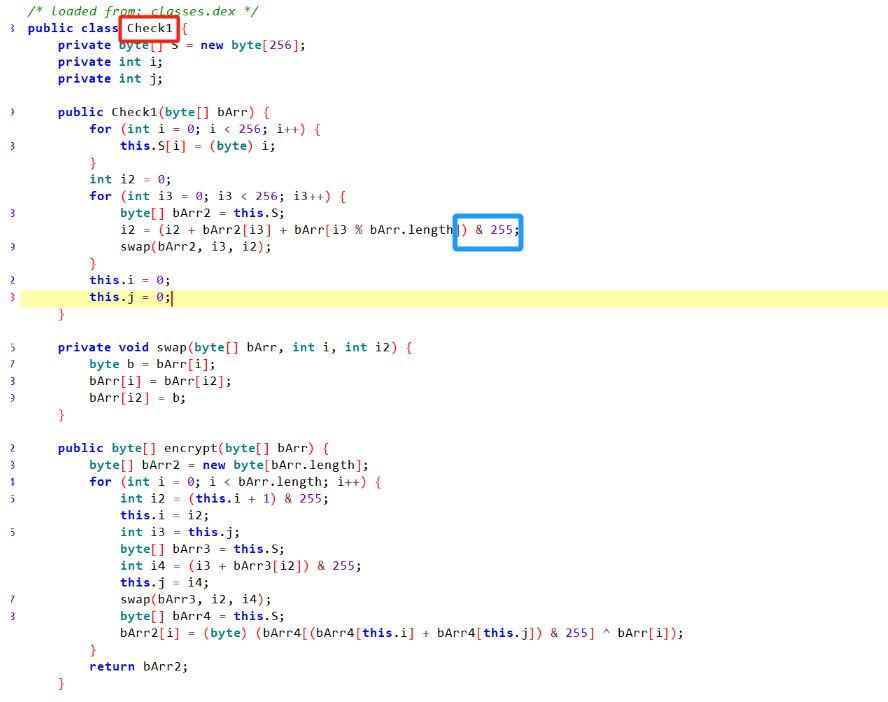
在rc4中，key通常为初始化函数的中间参数，可以快速找到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def rc4(data, key):
    S = list(range(256))
    j = 0
    out = []

    for i in range(256):
        j = (j + S[i] + key[i % len(key)]) % 256
        S[i], S[j] = S[j], S[i]

    i = j = 0
    for char in data:
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]
        out.append(char ^ S[(S[i] + S[j]) % 256])

    return bytes(out)


data = bytes([0x25, 0x6F, 0x3D, 0x6C, 0xF9, 0xE0, 0xCF, 0x3F, 0x2E, 0x24, 0xC6, 0x7B, 0x81, 0xBF, 0x55, 0x4F, 0x0D, 0x99, 0x87, 0x47, 0x48, 0xF7, 0xB9, 0x98, 0xFB, 0x1B, 0x22, 0xEC, 0x84, 0x23, 0xFD, 0xB2])
key = bytes([0x43]*18)
decrypted = rc4(data, key)
print(decrypted)

%128的魔改本质上就是8位二进制数组成的密钥变为7位

TEA

常规

一种对称算法，它使用64位明文（一组密文，232位）和128位密钥（一般是432位）进行加解密

TEA系列算法中均使用一个DELTA常数，但DELTA的值对算法并无什么影响，只是为了避免不良的取值，推荐DELTA的值十六进制值为0x9e3779B9，用于保证每一轮加密都不相同

标准加密流程

  1. 将明文按64位分组，将每个分组视为一个64位的二进制数，记为V
  2. 将128位的密钥分成4个32位的子密钥，分别记为K0、K1、K2、K3
  3. 将明文分组V分为两个32位的部分，分别记为V0和V1
  4. 设定一个32位的常数delta
  5. TEA算法的加密过程包括32轮迭代，每一轮的加密过程如下：

a. 首先，累加器sum被初始化为0

b. 接着，将delta值加到sum中。delta是一个常数，其值通常为0x9e3779b9，用于增加加密的随机性
c. 然后，将V1左移4位，加上K0，再异或上(V1+sum)和(V1右移5位+K1)的值。得到的结果作为V0的新值
d. 接下来，将V0左移4位，加上K2，再异或上(V0+sum)和(V0右移5位+K3)的值。得到的结果作为V1的新值
e. 重复上述步骤32次，即完成一轮迭代。在每一轮迭代中，V0和V1的值都会被更新，其中V1的更新依赖V0，而V0的更新依赖于V1

  1. 经过32轮迭代后，得到加密后的密文，记为C0和C1
  2. 将C0和C1按顺序连接起来，得到64位的密文

算法注意点

key一般为加密函数第二个参数，sum-=0x61c88647和sum+=0x9e3779b9是等价的

循环里的l和r一般用v0和v1，这样不容易弄混

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#define DELTA 0x9e3779b9

void tea_encrypt(unsigned int* v, unsigned int* key) {
    unsigned int l = v[0], r = v[1], sum = 0;
    for (size_t i = 0; i < 32; i++) {
        l += (((r << 4) ^ (r >> 5)) + r) ^ (sum + key[sum & 3]);
        sum += DELTA;
        r += (((l << 4) ^ (l >> 5)) + l) ^ (sum + key[(sum >> 11) & 3]); 
    }
    v[0] = l;
    v[1] = r;
}

//利用可逆性将加密过程逆转
void tea_decrypt(unsigned int* v, unsigned int* key) {
    unsigned int l = v[0], r = v[1], sum = 0;
    sum = DELTA * 32; l
    for (size_t i = 0; i < 32; i++) {
        r -= (((l << 4) ^ (l >> 5)) + l) ^ (sum + key[(sum >> 11) & 3]);
        sum -= DELTA;
        l -= (((r << 4) ^ (r >> 5)) + r) ^ (sum + key[sum & 3]);
    }
    v[0] = l;
    v[1] = r;
}

有些时候伪代码*4但实际上并不需要，因为这时的key是一个字节

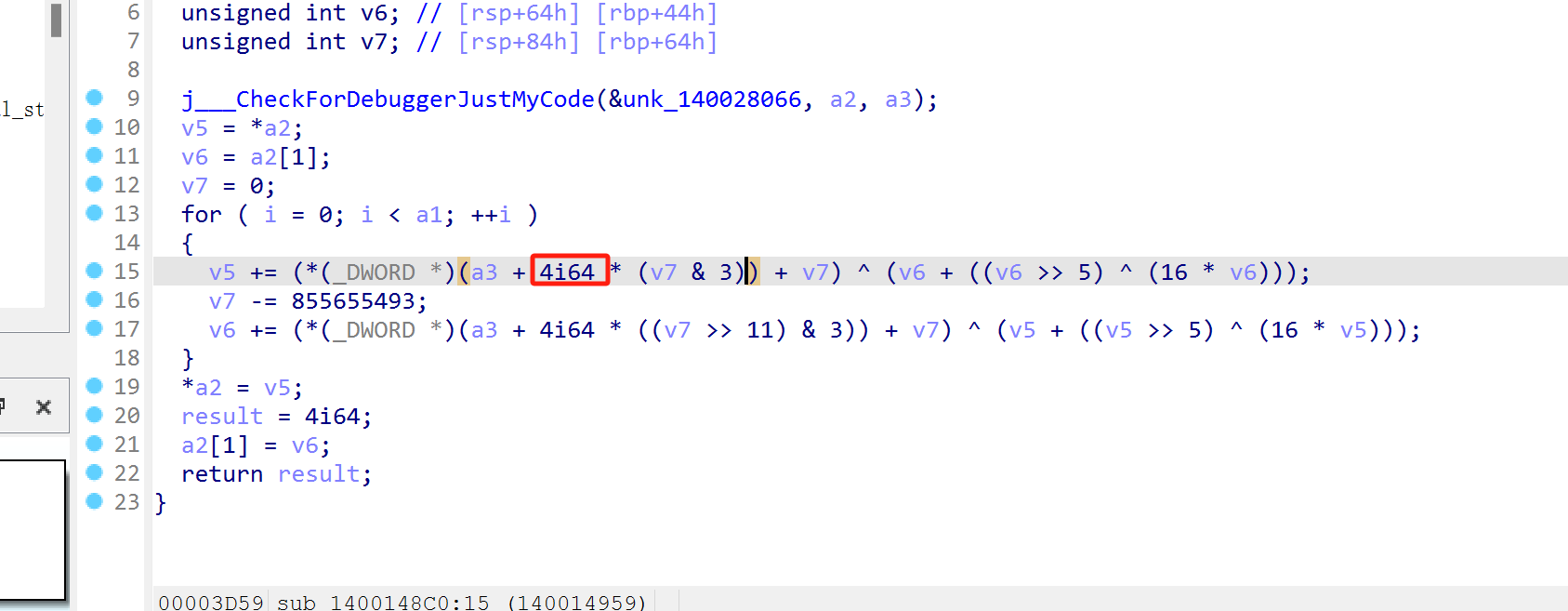
注意v0和v1到底是int还是unsigned int

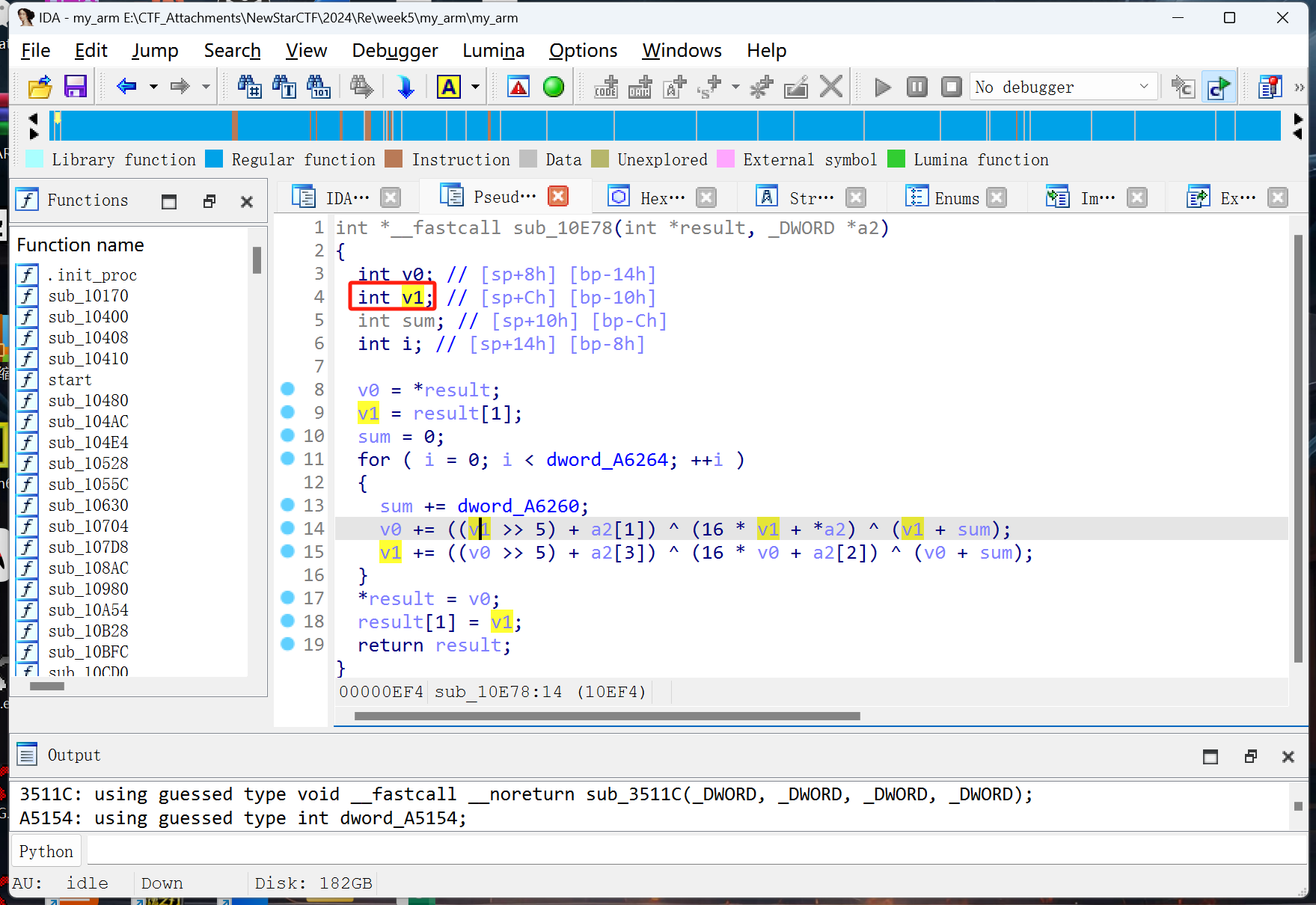
有多步操作的时候一定要注意写for循环的时候也要逆向，下面每次循环都要进行异或，自然得从后往前逆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>
#include <stdint.h>

void decrypt(uint32_t *v, uint32_t *k)
{
    uint32_t v0 = v[0], v1 = v[1], i;
    uint32_t delta = 0x9e3779b9;
    uint32_t sum = delta * 16;
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
    for (i = 0; i < 16; i++)
    {
        sum -= delta;
        v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
        v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);

    }
    v[0] = v0; v[1] = v1;
}

unsigned int enc[10] = {
    0xBC2B4DF9, 0x6213DD13, 0x89FFFCC9, 0x0FC94F7D, 0x526D1D63, 0xE341FD50, 0x97287633, 0x6BF93638, 
    0x83143990, 0x1F2CE22C
    };

unsigned int key[4] = {
    0x12345678, 0x09101112, 0x13141516, 0x15161718
    };

int main() {
    for (size_t i = 9; i >= 2; i-=2)
    {
        enc[i] ^= enc[1];
        enc[i - 1] ^= enc[0];
        decrypt(enc, key);
    }
    decrypt(enc, key);

    printf("%s", enc);
}
// DASCTF{I4TH0ok_I5S0ooFunny_Isnotit?????}

tea算法会有很多魔改的地方，比如循环次数，算法中多异或几个数，下面在tea的前后还实现了交换

如果算法里面异或i的话里面的循环也要逆着写

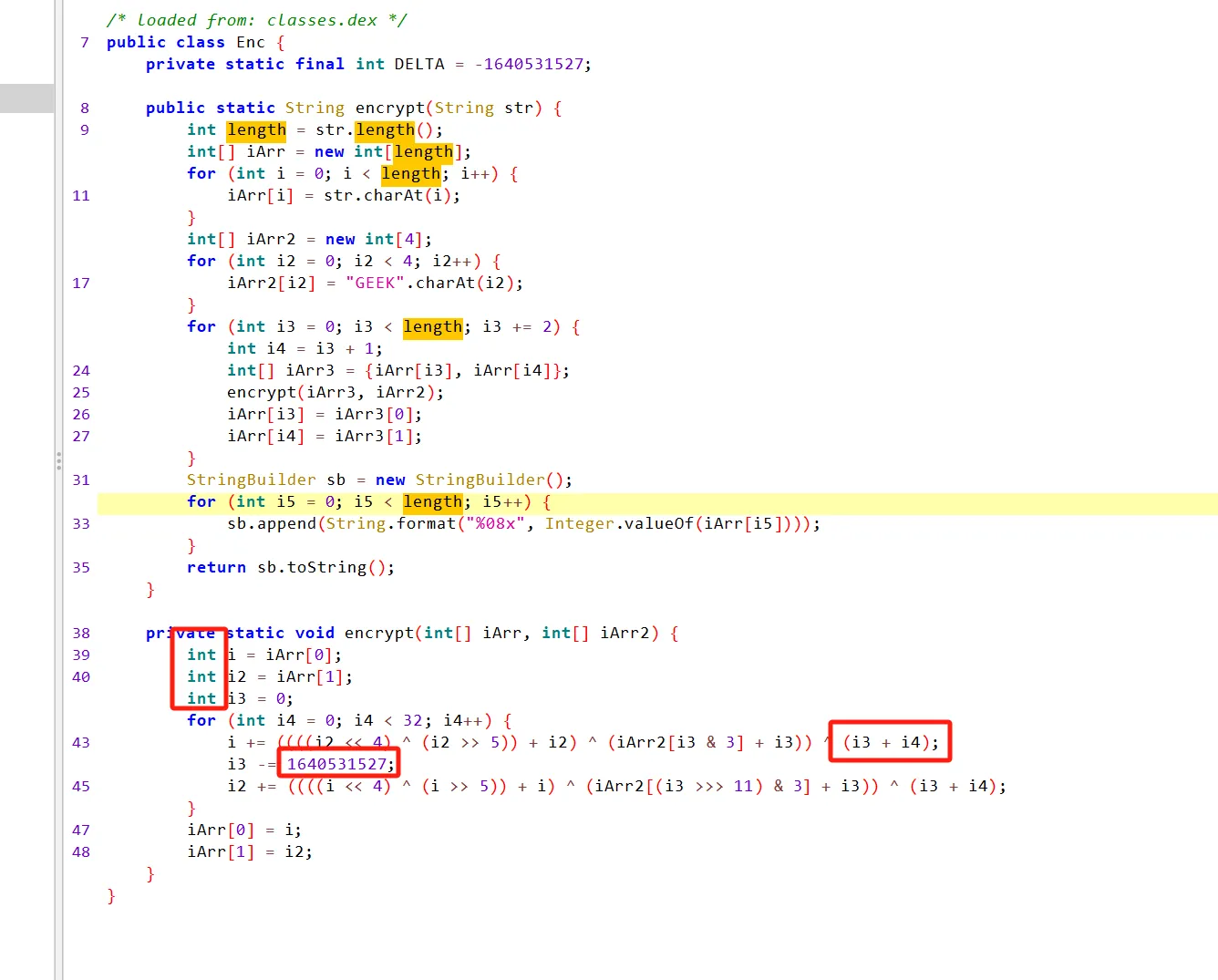
解密脚本

由于涉及内存指针等问题，大部分用c写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
void decrypt(uint32_t v[2], const uint32_t key[4]) {
    uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, delta = 0x9e3779b9;
    for (int i = 0; i < 32; i++) {
        v1 -= ((v0 << 4) + key[2]) ^ (v0 + sum) ^ ((v0 >> 5) + key[3]);
        v0 -= ((v1 << 4) + key[0]) ^ (v1 + sum) ^ ((v1 >> 5) + key[1]);
        sum -= delta;
    }
    v[0] = v0;
    v[1] = v1;
}

int main() {
    uint32_t key[4] = {0x11121314, 0x22232425, 0x33343536, 0x41424344};
    uint32_t v5[8] = {0x38b97e28, 0xb7e510c1, 0xb4b29fae, 0x5593bbd7,0x3c2e9b9e, 0x1671c637, 0x8f3a8cb5, 0x5116e515};

    for (int i = 0; i < 8; i += 2) {
        decrypt(&v5[i], key);
    }
	
	for (int i = 0; i < 8; i++) {
        for (int m = 0; m <= 3; m++) {
            printf("%c", (v5[i] >> (8 * m)) & 0xff);
        }
    }

    return 0;
}

tea加密的另一种模式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
void decrypt(uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0 = v[0], v1 = v[1], delta = 0x61C88747, sum = delta * (-64);
    for (i=0; i < 64; i++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3])^v0;
        sum += delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3])^v1;

    }
    v[0] = v0; v[1] = v1;
}

int main() {
    uint32_t const k[4] = {0x5377654E,0x21726174,0x5377654E,0x21726174};
    uint32_t enc[] = {0xC19EA29C,0xDC091F87,0x91F6E33B,0xF69A5C7A,0x93529F20,0x8A5B94E1,0xF91D069B,0x23B0E340};
    for(int i=0; i<8; i+=2){
        decrypt(&enc[i], k);
    }
    for (int i = 0; i < 8; i++) {
        for (int m = 0; m <= 3; m++) {
            printf("%c", (v5[i] >> (8 * m)) & 0xff);
        }
    }
    return 0;
}

XTEA

从做题角度来说差别不大

XXTEA

相比xtea与tea，xxtea的复杂度更上了一层，subkey的方式变为已进行的轮数的最后两位与delta叠加的最后两位相异或，delta迭代与tea相同，常见是9轮循环，循环里面先q再p，q就是循环的次数，为6+52/(n+1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#define MX (((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4))) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z))
#define DELTA 0x9e3779b9

//XXTEA 加密，在处理数据流中每个数据时利用了相邻数据，使用MX函数计算加密值
static uint32_t * xxtea_uint_encrypt(uint32_t * data, size_t len, uint32_t * key) {
    uint32_t n = (uint32_t)len - 1;
    uint32_t z = data[n], y, p, q = 6 + 52 / (n + 1), sum = 0, e;

    if (n < 1) return data;

    while (0 < q--) {
        sum += DELTA;
        // 根据sum 计算得出0~3中的某一个数值, 用于MX中与p共同作用选择key数组中某个秘钥值
        e = sum >> 2 & 3;

        //遍历每个待加密的数据
        for (p = 0; p < n; p++) {
            //z的初值为data[len - 1]，即将数据数组当做是环形队列来处理的，首尾相连，当加密data[0]时，需要用到data[len - 1]，data[0]，data[0 + 1]，以及MX计算返回的的一个加密值，加密值与data[0]相加后达到加密的效果
            y = data[p + 1];
            z = data[p] += MX;
        }

        //当加密data[len-1]时，需要用到data[len - 2]，data[len-1]，data[0]，以及MX计算返回的的一个加密值，加密值与data[len-1]相加后达到加密的效果
        y = data[0];
        z = data[n] += MX;
    }

    return data;
}

static uint32_t * xxtea_uint_decrypt(uint32_t * data, size_t len, uint32_t * key) {
    uint32_t n = (uint32_t)len - 1;
    uint32_t z, y = data[0], p, q = 6 + 52 / (n + 1), sum = q * DELTA, e;

    if (n < 1) return data;

    while (sum != 0) {
        e = sum >> 2 & 3;

        for (p = n; p > 0; p--) {
            z = data[p - 1];
            y = data[p] -= MX;
        }

        z = data[n];
        y = data[0] -= MX;
        sum -= DELTA;
    }

    return data;
}

有些没6+52/(n+1)，但还是有其他特征,而且delta也很明显

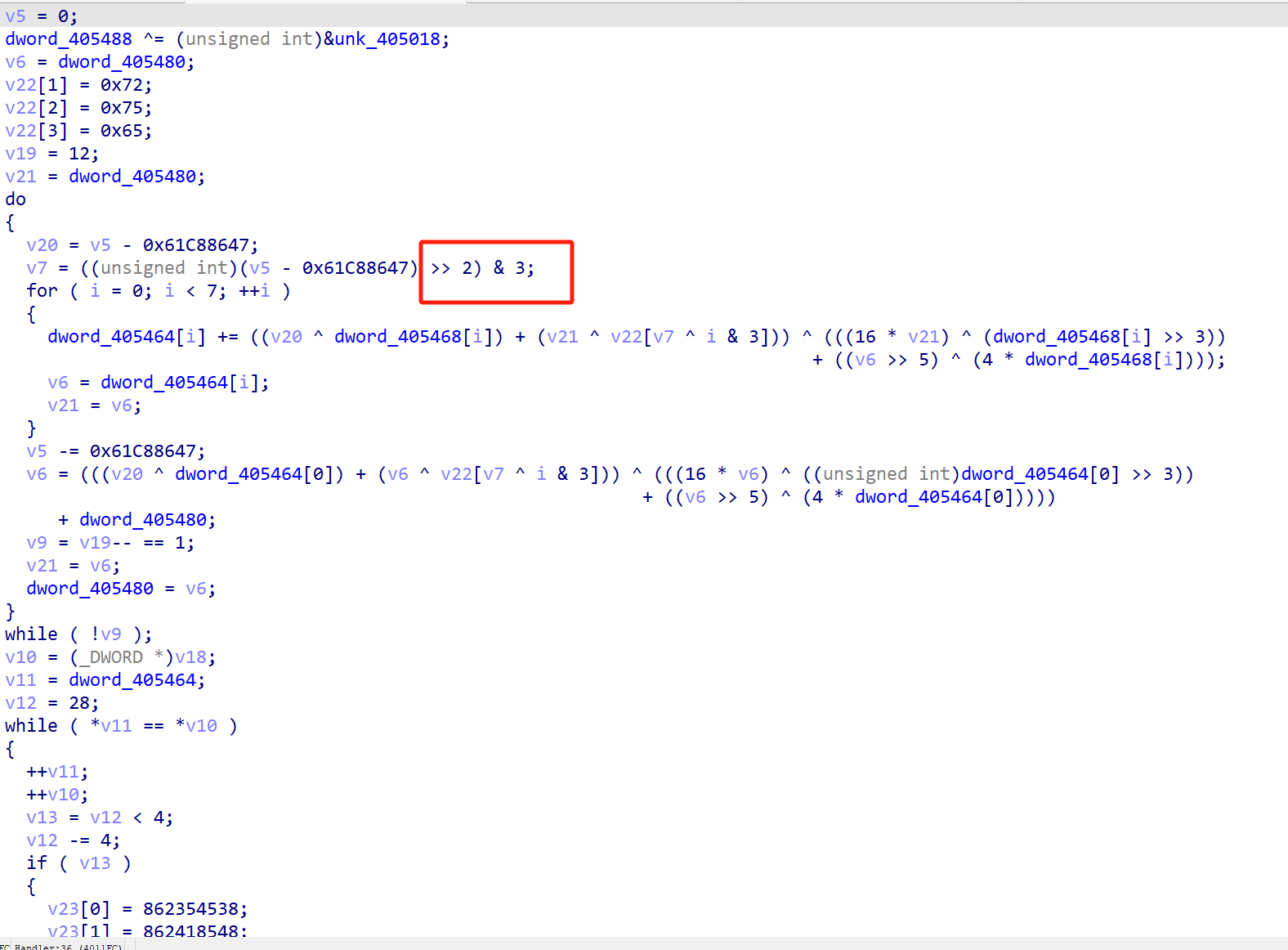
下面是运行脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))

void btea(uint32_t *v, int n, uint32_t const key[4]) {
    uint32_t y, z, sum;
    unsigned p, rounds, e;
    if (n > 1) { //加密函数
        rounds = 6 + 52 / n;
        sum = 0;
        z = v[n - 1];
        do {
            sum += DELTA;
            e = (sum >> 2) & 3;
            for (p = 0; p < n - 1; p++) {
                y = v[p + 1];
                z = v[p] += MX;
            }
            y = v[0];
            z = v[n - 1] += MX;
        } while (--rounds);
    } else if (n < -1) {  //解密函数
        n = -n;
        rounds = 6 + 52 / n;
        sum = rounds * DELTA;
        y = v[0];
        do {
            e = (sum >> 2) & 3;
            for (p = n - 1; p > 0; p--) {
                z = v[p - 1];
                y = v[p] -= MX;
            }
            z = v[n - 1];
            y = v[0] -= MX;
            sum -= DELTA;
        } while (--rounds);
    }
}

int main() {
    uint32_t v[9] = {689085350, 626885696, 1894439255, 1204672445, 1869189675, 475967424, 1932042439, 1280104741, 2808893494};
    uint32_t const k[4] = {12345678, 12398712, 91283904, 12378192};
    int n = 9;
    btea(v, -n, k);
    for (int i = 0; i < 9; i ++) {
        printf("%c", v[i] & 0xff);
        printf("%c", v[i] >> 8 & 0xff);
        printf("%c", v[i] >> 16 & 0xff);
        printf("%c", v[i] >> 24 & 0xff);
    }
    printf("\n");
    return 0;
}
import base64
from ctypes import *

enc="F8URvwNjuAYMN6GVXvgJE1Oe2ULWWow0WThUe0k95xTg60OY"
data=list(base64.b64decode(enc))
enc=[int.from_bytes(data[i:i + 4], "little") for i in range(0,len(data),4)]
key=list(map(ord,"0M21I908n117gC1~"))
key=[int.from_bytes(key[i:i + 4], "little") for i in range(0,len(key),4)]


def MX(z, y, sum1, k, p, e):
    return   c_uint32(((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[(p&3)^e.value]^z.value)))
def btea(v,k,n,delta):

    if n>1:
        sum1=c_uint32(0)
        z=c_uint32(v[n-1])
        rounds=6+52//n
        e=c_uint32(0)

        while rounds>0:
            sum1.value+=delta
            e.value=((sum1.value>>2)&3)
            for p in range(n-1):
                y=c_uint32(v[p+1])
                v[p] = c_uint32(v[p] + MX(z,y,sum1,k,p,e).value).value
                z.value=v[p]

            y=c_uint32(v[0])
            v[n-1] = c_uint32(v[n-1] + MX(z,y,sum1,k,n-1,e).value).value
            z.value=v[n-1]
            rounds-=1
    else:
        sum1=c_uint32(0)
        n=-n
        rounds=6+52//(n+1)
        sum1.value=rounds*delta
        y=c_uint32(v[0])
        e=c_uint32(0)

        while rounds>0:
            e.value=((sum1.value>>2)&3)
            for p in range(n-1, 0, -1):
                z=c_uint32(v[p-1])
                v[p] = c_uint32(v[p] - MX(z,y,sum1,k,p,e).value).value
                y.value=v[p]

            z=c_uint32(v[n-1])
            v[0] = c_uint32(v[0] - MX(z,y,sum1,k,0,e).value).value
            y.value=v[0]
            sum1.value-=delta
            rounds-=1

    return v

if __name__=='__main__':
    a=enc
    k= key
    delta=0x9e3779b9
    n=len(a)
    res=btea(a,k,-n,delta)
    flag=''
    import libnum
    for i in res:
        flag+=(libnum.n2s(i)[::-1].decode())
    print("ISCC{"+flag.strip()+"}")

AES

参考链接： https://zhuanlan.zhihu.com/p/78913397

算法

AES算法主要有四种操作处理，分别是密钥加法层、字节代换层、行位移层、列混淆层。而明文x和密钥k都是由16个字节组成的数据

AES算法在处理的轮数上只有最后一轮操作与前面的轮处理上有些许不同，在轮处理开始前还单独进行了一次轮密钥加的处理。在处理轮数上，我们只考虑128位密钥的10轮处理

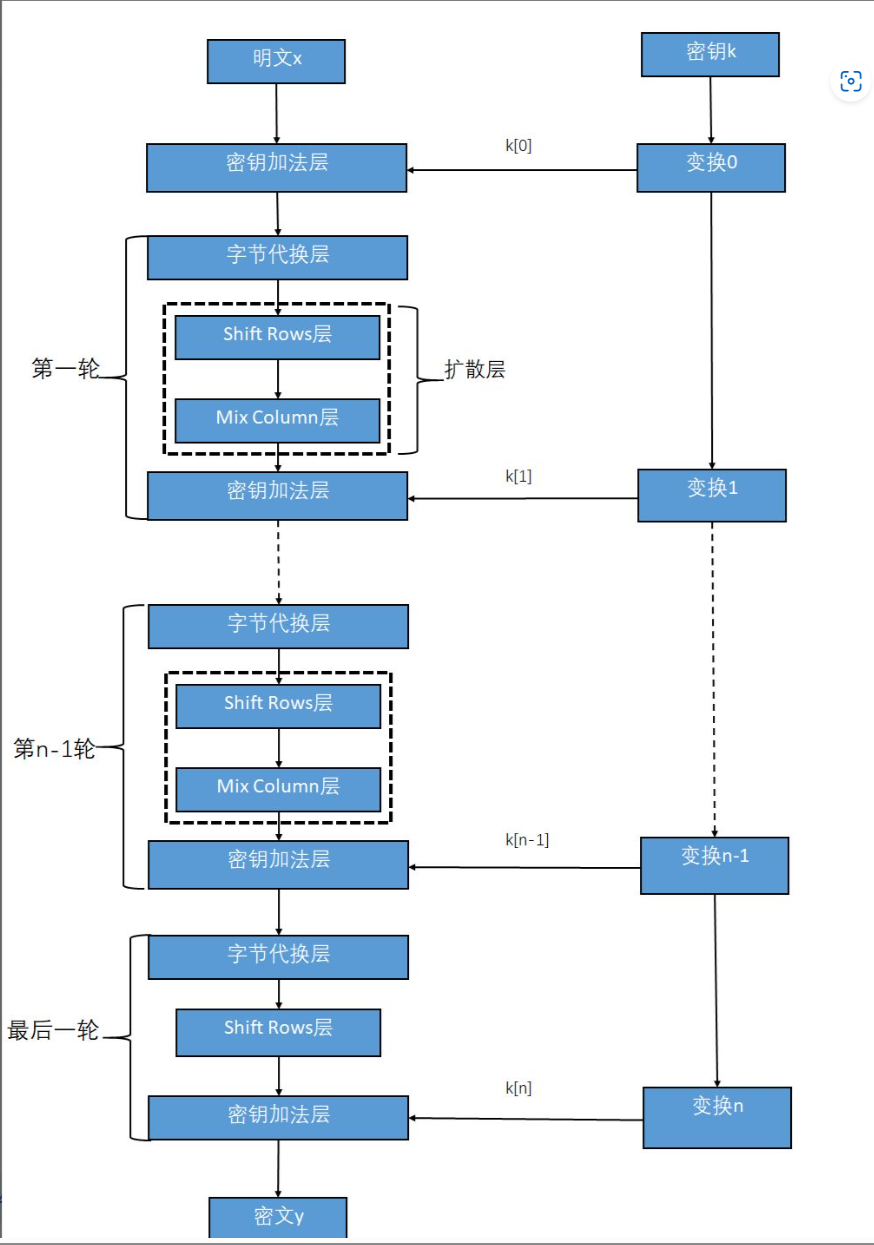
字节代换

S_box表是通过某种方法计算出来的。S_box表是一个拥有256个字节元素的数组，可以将其定义为一维数组，也可以将其定义为16×16的二维数组，如果将其定义为二维数组，读取S_box数据的方法就是要将输入数据的每个字节的高四位作为第一个下标，低四位作为第二个下标，从s盒中取出并赋给字符

s盒和逆s盒

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
unsigned char S[256] = {
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16};
unsigned char inv_S[256] = {
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D};

特征值：>>4 &0xF

行位移

只在4×4矩阵的行间进行操作，每行4字节的数据。在加密时，保持矩阵的第一行不变，第二行向左移一个字节、第三行向左移2个字节、第四行向左移3个字节

特征值：三个>>和<<

也可以这样，这个真有点抽象

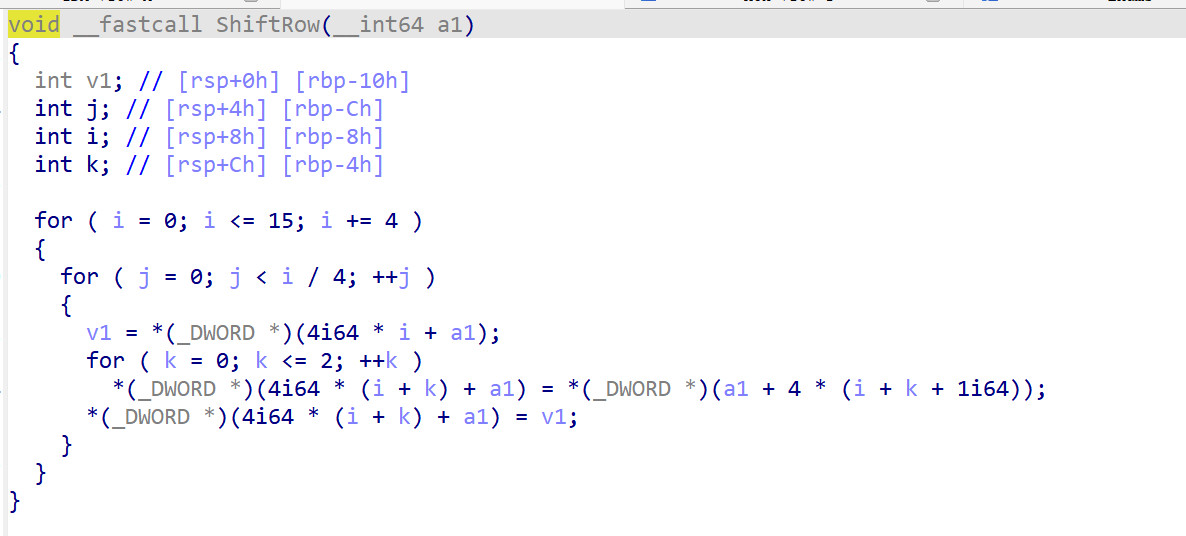
列混淆

在加密的正向列混淆中，我们要将输入的4·4矩阵左乘一个给定的4·4矩阵。而它们之间的加法、乘法都在扩展域GF(2^8)中进行，所以也就可以将这一个步骤分成两个部分进行讲解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
const unsigned char MixArray[4][4] =
{
    0x02, 0x03, 0x01, 0x01,
    0x01, 0x02, 0x03, 0x01,
    0x01, 0x01, 0x02, 0x03,
    0x03, 0x01, 0x01, 0x02
    };

int MixColum(unsigned char(*PlainArray)[4])
{
    int ret = 0;

    unsigned char ArrayTemp[4][4];

    memcpy(ArrayTemp, PlainArray, 16);

        for (int i = 0; i < 4; i++)
    {
            for (int j = 0; j < 4; j++)
        {
            PlainArray[i][j] =
            MixArray[i][0] * ArrayTemp[0][j] +
            MixArray[i][1] * ArrayTemp[1][j] +
            MixArray[i][2] * ArrayTemp[2][j] +
            MixArray[i][3] * ArrayTemp[3][j];
        }
    }
    return ret;
}

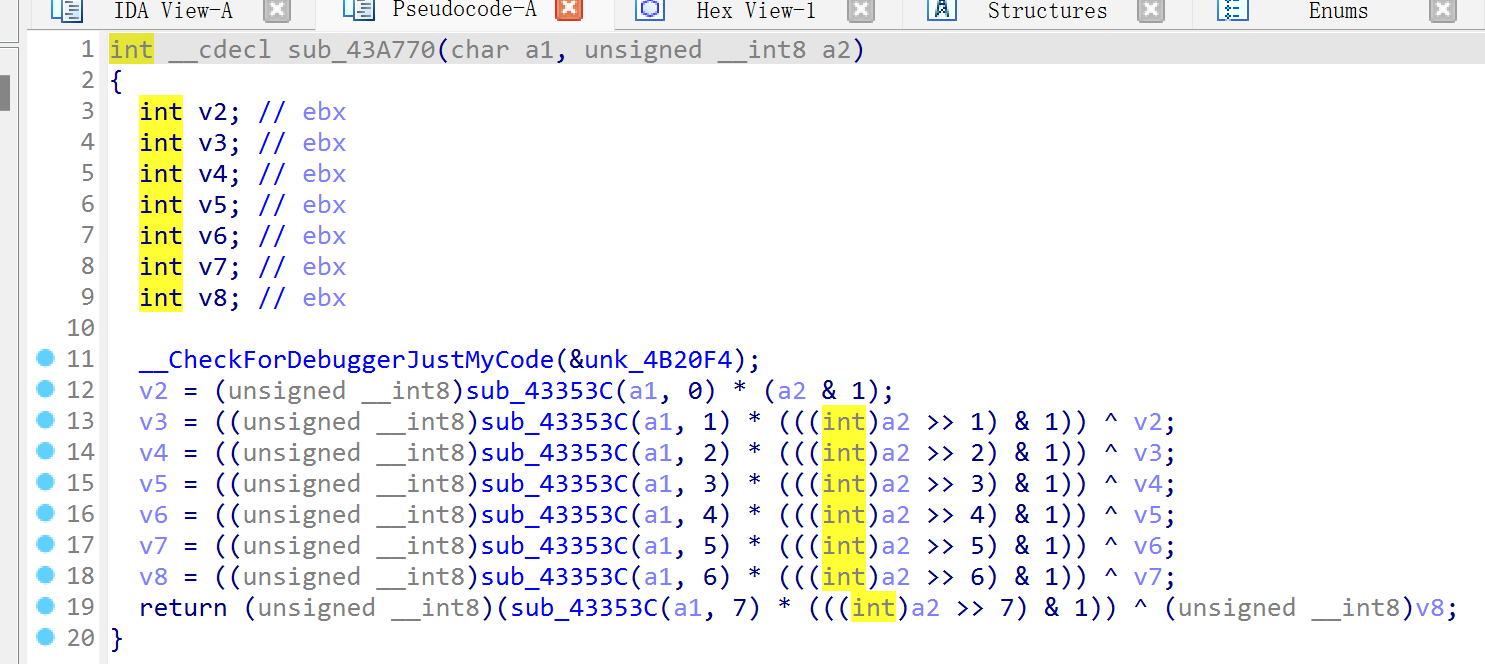
轮密钥加

在密钥加法层中有两个输入的参数，分别是明文和子密钥k，而且这两个输入都是128位的。在%2的扩展域中加减法与异或运算等价，所以这里只需异或

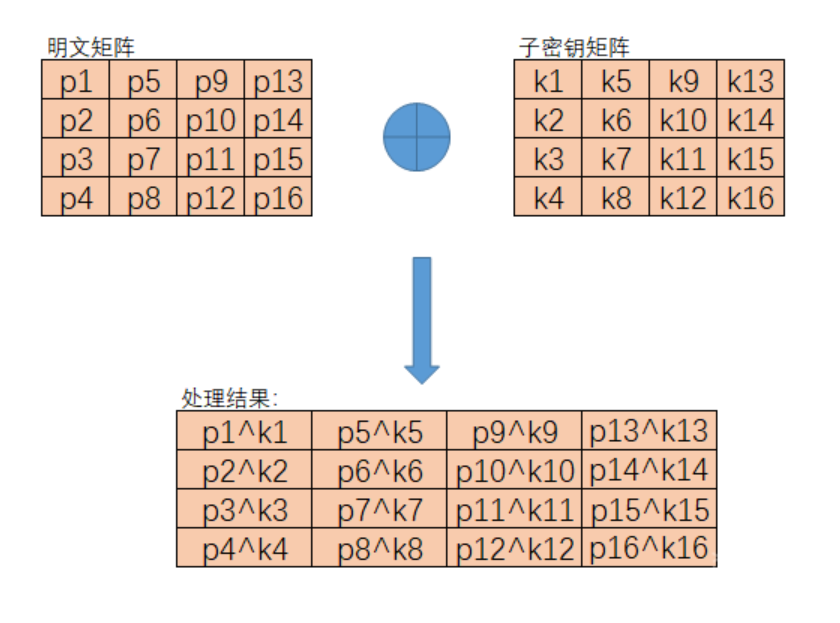
密钥生成

子密钥的生成是以列为单位进行的，一列是32Bit，四列组成子密钥共128Bit。生成子密钥的数量比AES算法的轮数多一个，因为第一个密钥加法层进行密钥漂白时也需要子密钥。密钥漂白是指在AES的输入盒输出中都使用的子密钥的XOR加法。子密钥在图中都存储在W[0]、W[1]…W[43]的扩展密钥数组之中

k1-k16表示原始密钥对应的字节，而图中子密钥k0与原始子密钥相同。在生成的扩展密钥中W的下标如果是4的倍数时(从零开始)需要对异或的参数进行G函数处理

扩展密钥生成有关公式如下

1
2
3
4
1<= i <= 10
1<= j <= 3
W[4i] = W[4(i-1)] ^ T(W[4i-1]);
W[4i+j] = W[4(i-1)+j] ^ W[4i-1+j];

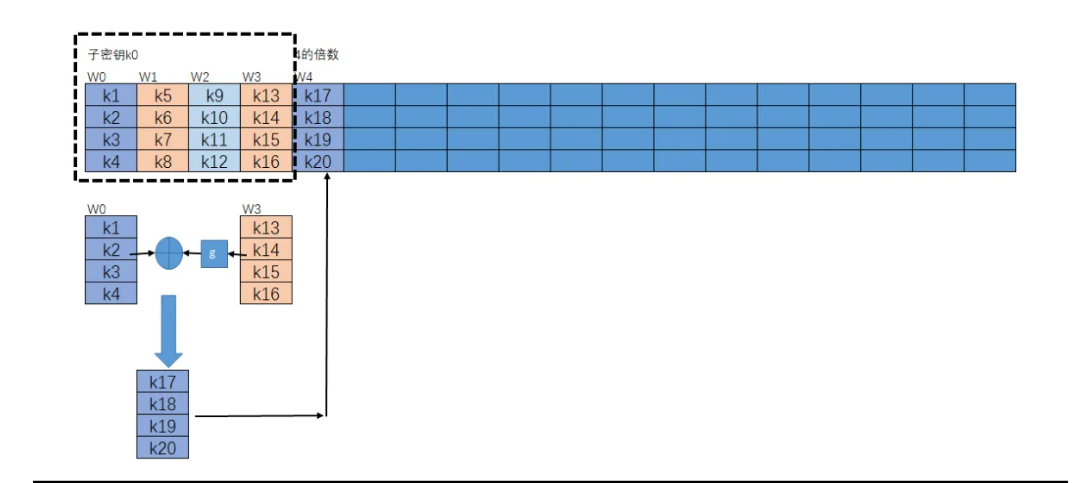
T函数实现较复杂

填充

几种典型的填充方式：

NoPadding： 不做任何填充，但是要求明文必须是16字节的整数倍

PKCS5Padding（默认）： 如果明文块少于16个字节，在明文块末尾补足相应数量的字符，且每个字节的值等于缺少的字符数。 比如明文：{1,2,3,4,5,a,b,c,d,e},缺少6个字节，则补全为{1,2,3,4,5,a,b,c,d,e,6,6,6,6,6,6 }

ISO10126Padding：如果明文块少于16个字节（128bit），在明文块末尾补足相应数量的字节，最后一个字符值等于缺少的字符数，其他字符填充随机数。比如明文：{1,2,3,4,5,a,b,c,d,e},缺少6个字节，则可能补全为{1,2,3,4,5,a,b,c,d,e,5,c,3,G,$,6}

PKCS7Padding原理与PKCS5Padding相似，区别是PKCS5Padding的blocksize为8字节，而PKCS7Padding的blocksize可以为1到255字节

模式

AES的工作模式，体现在把明文块加密成密文块的处理过程中。AES加密算法提供了五种不同的工作模式：CBC,ECB,CTR,CFB,OFB

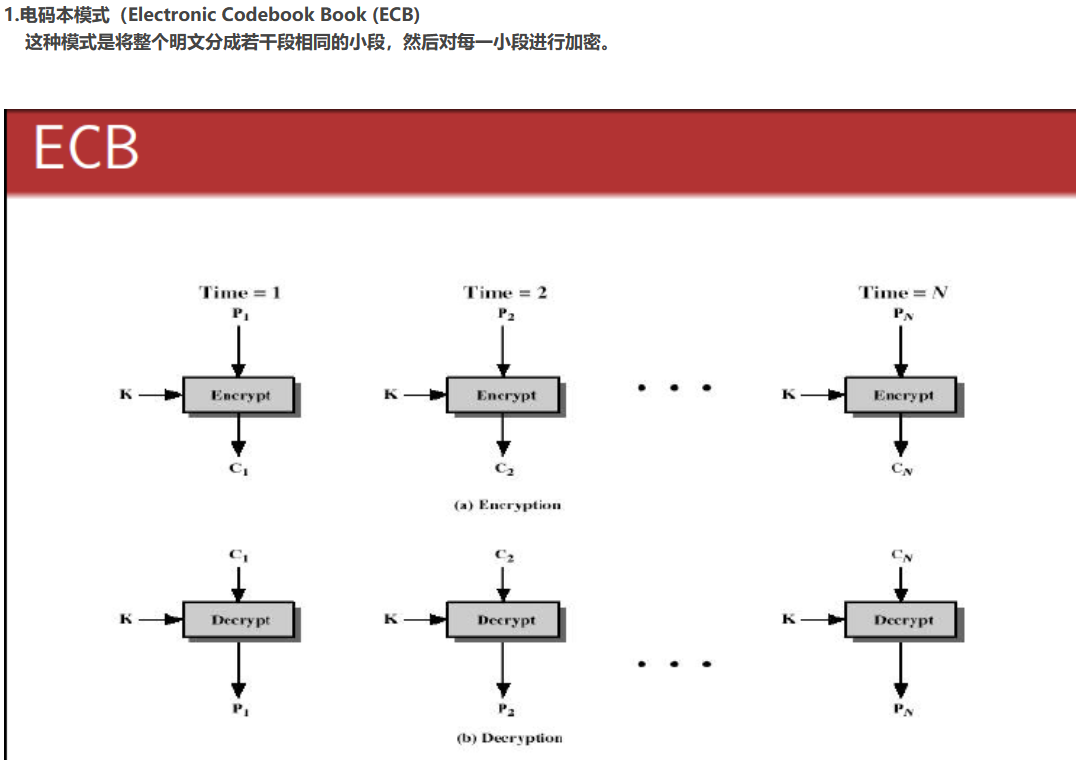
适合加密随机数据

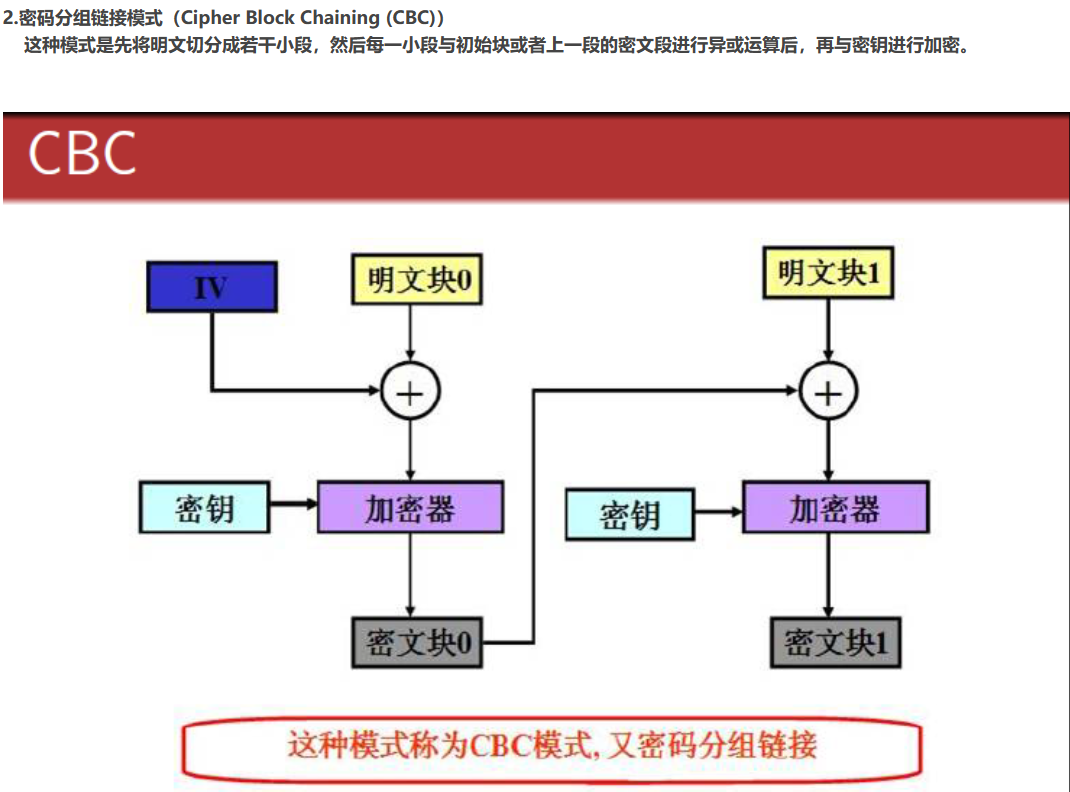
适合软件加密:CFB,OFB,CTR

代码

标准aes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import base64
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad

key = 0x554B134A029DE539438BD18604BF114

key_bytes = key.to_bytes(16, byteorder='big')
print(key_bytes)

encrypted_data = "2e8Ugcv8lKVhL3gkv3grJGNE3UqkjlvKqCgJSGRNHHEk98Kd0wv6s60GpAUsU+8Q"

encrypted_bytes = base64.b64decode(encrypted_data)


cipher = AES.new(key_bytes, AES.MODE_ECB)

try:
    decrypted_data = unpad(cipher.decrypt(encrypted_bytes), AES.block_size)

    print("解密结果:", decrypted_data.decode('utf-8'))
except (ValueError, KeyError):
    print("解密失败或填充错误！")

这是修改s盒的代码，密文只能16位一组解密，密文按顺序提取unspaced即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
class IAES:
    global new_s_box
    def __init__(self):
        self.Nk = 4
        self.Nb = 4
        self.Nr = 10

    def arrays(self, raws):
        Nb = []
        for i in range(4):
            Nb = Nb + [raws[4 * 0 + i], raws[4 * 1 + i], raws[4 * 2 + i], raws[4 * 3 + i]]
        return Nb

    def Inv_arrays(self, raws):
        Inv_raws = []
        for i in range(4):
            Inv_raws = Inv_raws + [raws[4 * 0 + i], raws[4 * 1 + i], raws[4 * 2 + i], raws[4 * 3 + i]]
        return Inv_raws

    def view(self, raws):
        raws = self.Inv_arrays(raws)
        raws = ''.join([x.to_bytes(1, byteorder='big').hex() for x in raws])
        print(raws)

    def view2(self, list):
        for i in range(len(list)):
            print(format(list[i], '2x'), end=' ')
            if i & 3 == 3:  # i%4 == 3
                print('\n', end='')
        print('\n', end='')

    def AddRoundKey(self, raws, Keys):
        AddRoundKey = []
        for raw, Key in zip(raws, Keys):
            AddRoundKey.append(raw ^ Key)
        return AddRoundKey

    def SubBytes(self, raws):
        S_box=new_s_box
        raws_S_box = []
        for raw in raws:
            raws_S_box.append(S_box[raw])
        return raws_S_box

    def InvSubBytes(self, raws,inv_s_box):
        IS_box = inv_s_box
        raws_IS_box = []
        for raw in raws:
            raws_IS_box.append(IS_box[raw])
        return raws_IS_box

    def InvShiftRows(self, raws):
        s13 = raws.pop(7)
        raws.insert(4, s13)
        s2223 = raws[10:12]
        del raws[10:12]
        raws[8:0] = s2223
        s313233 = raws[13:16]
        del raws[13:16]
        raws[12:0] = s313233
        return raws

    def GMUL(self, a, b):  # Russian Peasant Multiplication algorithm
        p = 0
        while a and b:
            if b & 1:  # b%2
                p = p ^ a
            if a & 0x80:  # a=a*x^7(a>0),a >= 2**7(128)
                a = (a << 1) ^ 0x11b  # 0x11b = x^8 + x^4 + x^3 + x + 1 (0b100011011)
            else:
                a = a << 1
            b = b >> 1
        return p

    def InvMixColumns(self, raws):
        for i in range(4):
            raws[0 * 4 + i], \
                raws[1 * 4 + i], \
                raws[2 * 4 + i], \
                raws[3 * 4 + i] \
                = \
                self.GMUL(0x0e, raws[0 * 4 + i]) ^ self.GMUL(0x0b, raws[1 * 4 + i]) ^ self.GMUL(0x0d, raws[
                    2 * 4 + i]) ^ self.GMUL(0x09, raws[3 * 4 + i]), \
                self.GMUL(0x09, raws[0 * 4 + i]) ^ self.GMUL(0x0e, raws[1 * 4 + i]) ^ self.GMUL(0x0b, raws[
                    2 * 4 + i]) ^ self.GMUL(0x0d, raws[3 * 4 + i]), \
                self.GMUL(0x0d, raws[0 * 4 + i]) ^ self.GMUL(0x09, raws[1 * 4 + i]) ^ self.GMUL(0x0e, raws[
                    2 * 4 + i]) ^ self.GMUL(0x0b, raws[3 * 4 + i]), \
                self.GMUL(0x0b, raws[0 * 4 + i]) ^ self.GMUL(0x0d, raws[1 * 4 + i]) ^ self.GMUL(0x09, raws[
                    2 * 4 + i]) ^ self.GMUL(0x0e, raws[3 * 4 + i])
        return raws

    def RotWord(self, temp):
        b0 = temp.pop(0)
        temp.insert(3, b0)
        return temp

    def SubWord(self, temp):
        temp = self.SubBytes(temp)
        return temp

    def KeyExpansion(self, key):
        i = 0
        w = [[0]] * (self.Nb * (self.Nr + 1))
        Rcon = [[0x01, 0x00, 0x00, 0x00],
                [0x02, 0x00, 0x00, 0x00],
                [0x04, 0x00, 0x00, 0x00],
                [0x08, 0x00, 0x00, 0x00],
                [0x10, 0x00, 0x00, 0x00],
                [0x20, 0x00, 0x00, 0x00],
                [0x40, 0x00, 0x00, 0x00],
                [0x80, 0x00, 0x00, 0x00],
                [0x1B, 0x00, 0x00, 0x00],
                [0x36, 0x00, 0x00, 0x00]
                ]
        while i < self.Nk:
            w[i] = ([key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]])
            i = i + 1

        i = self.Nk

        while i < self.Nb * (self.Nr + 1):
            temp = w[i - 1].copy()
            if i % self.Nk == 0:
                temp = self.SubWord(self.RotWord(temp))
                temp2 = []
                for temp1, Rcon1 in zip(temp, Rcon[(i // self.Nk) - 1]):
                    temp2.append(temp1 ^ Rcon1)
                temp = temp2
            elif self.Nk > 6 and i % self.Nk == 4:
                temp = self.SubWord(temp)
            w_temp = []
            for w1, temp1 in zip(w[i - self.Nk], temp):
                w_temp.append(w1 ^ temp1)
            w[i] = w_temp
            i = i + 1
        return w

    def IAES(self, IInput, Cipher_Key,inv_s_box):
        IInput = [IInput1 for IInput1 in IInput]
        Cipher_Key = [Cipher_Key1 for Cipher_Key1 in Cipher_Key]
        KeyExpansion = self.KeyExpansion(Cipher_Key)
        keys = []
        for Key_index in range(len(KeyExpansion) // 4):
            keys_temp = (KeyExpansion[4 * Key_index] + KeyExpansion[4 * Key_index + 1] + KeyExpansion[
                4 * Key_index + 2] + KeyExpansion[4 * Key_index + 3])
            keys_temp = self.arrays(keys_temp)
            keys.append(keys_temp)
        IInput = self.arrays(IInput)
        self.view(IInput)
        self.view(keys[-1])
        IInput = self.AddRoundKey(IInput, keys[-1])
        self.view(IInput)
        for index in range(self.Nr - 1):
            IInput = self.InvShiftRows(IInput)
            self.view(IInput)
            IInput = self.InvSubBytes(IInput,inv_s_box)
            self.view(IInput)
            self.view(keys[-1 - 1 - index])
            IInput = self.AddRoundKey(IInput, keys[-1 - 1 - index])
            self.view(IInput)
            IInput = self.InvMixColumns(IInput)
            self.view(IInput)
        IInput = self.InvShiftRows(IInput)
        self.view(IInput)
        IInput = self.InvSubBytes(IInput,inv_s_box)
        self.view(IInput)
        self.view(keys[0])
        IInput = self.AddRoundKey(IInput, keys[0])
        self.view(IInput)
        IInput = self.Inv_arrays(IInput)
        IInput = bytes(IInput)
        return IInput


S_box = [
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
]

new_s_box = [0x31, 0x52, 0x5A, 0xC8, 0x0B, 0xAC, 0xF3, 0x3A, 0x8B, 0x54, 0x27, 0x9B, 0xAB, 0x95, 0xDE, 0x83, 0x60, 0xCB,
             0x53, 0x7F, 0xC4, 0xE3, 0x0A, 0x97, 0xE0, 0x29, 0xD5, 0x68, 0xC5, 0xDF, 0xF4, 0x7B, 0xAA, 0xD6, 0x42, 0x78,
             0x6C, 0xE9, 0x70, 0x17, 0xD7, 0x37, 0x24, 0x49, 0x75, 0xA9, 0x89, 0x67, 0x03, 0xFA, 0xD9, 0x91, 0xB4, 0x5B,
             0xC2, 0x4E, 0x92, 0xFC, 0x46, 0xB1, 0x73, 0x08, 0xC7, 0x74, 0x09, 0xAF, 0xEC, 0xF5, 0x4D, 0x2D, 0xEA, 0xA5,
             0xDA, 0xEF, 0xA6, 0x2B, 0x7E, 0x0C, 0x8F, 0xB0, 0x04, 0x06, 0x62, 0x84, 0x15, 0x8E, 0x12, 0x1D, 0x44, 0xC0,
             0xE2, 0x38, 0xD4, 0x47, 0x28, 0x45, 0x6E, 0x9D, 0x63, 0xCF, 0xE6, 0x8C, 0x18, 0x82, 0x1B, 0x2C, 0xEE, 0x87,
             0x94, 0x10, 0xC1, 0x20, 0x07, 0x4A, 0xA4, 0xEB, 0x77, 0xBC, 0xD3, 0xE1, 0x66, 0x2A, 0x6B, 0xE7, 0x79, 0xCC,
             0x86, 0x16, 0xD0, 0xD1, 0x19, 0x55, 0x3C, 0x9F, 0xFB, 0x30, 0x98, 0xBD, 0xB8, 0xF1, 0x9E, 0x61, 0xCD, 0x90,
             0xCE, 0x7C, 0x8D, 0x57, 0xAE, 0x6A, 0xB3, 0x3D, 0x76, 0xA7, 0x71, 0x88, 0xA2, 0xBA, 0x4F, 0x3E, 0x40, 0x64,
             0x0F, 0x48, 0x21, 0x35, 0x36, 0x2F, 0xE8, 0x14, 0x5D, 0x51, 0xD8, 0xB5, 0xFE, 0xD2, 0x96, 0x93, 0xA1, 0xB6,
             0x43, 0x0D, 0x4C, 0x80, 0xC9, 0xFF, 0xA3, 0xDD, 0x72, 0x05, 0x59, 0xBF, 0x0E, 0x26, 0x34, 0x1F, 0x13, 0xE5,
             0xDC, 0xF2, 0xC6, 0x50, 0x1E, 0xE4, 0x85, 0xB7, 0x39, 0x8A, 0xCA, 0xED, 0x9C, 0xBB, 0x56, 0x23, 0x1A, 0xF0,
             0x32, 0x58, 0xB2, 0x65, 0x33, 0x6F, 0x41, 0xBE, 0x3F, 0x6D, 0x11, 0x00, 0xAD, 0x5F, 0xC3, 0x81, 0x25, 0xA8,
             0xA0, 0x9A, 0xF6, 0xF7, 0x5E, 0x99, 0x22, 0x2E, 0x4B, 0xF9, 0x3B, 0x02, 0x7A, 0xB9, 0x5C, 0x69, 0xF8, 0x1C,
             0xDB, 0x01, 0x7D, 0xFD]

new_contrary_sbox = [0] * 256

for i in range(256):
    line = (new_s_box[i] & 0xf0) >> 4

    rol = new_s_box[i] & 0xf

    new_contrary_sbox[(line * 16) + rol] = i

print(new_contrary_sbox)
IInput = bytes.fromhex('B0CC93EAE92FEF5699396E023B4F9E42')
print(IInput)
Cipher_Key = bytes(b'user01_nkctf2024')
print(Cipher_Key)
Out = IAES().IAES(IInput, Cipher_Key,new_contrary_sbox)
print(Out)

DES

对称密码，DES使用64位的密钥和64位的明文块进行加密。DES算法的分组大小是64位，因此，如果需要加密的明文长度不足64位，需要进行填充；如果明文长度超过64位，则需要使用分组模式进行分组加密

识别主要靠常量

初始置换(IP置换)

将输入的64位明文块进行置换和重新排列，生成新的64位数据块

目的:增加加密的混乱程度，使明文中的每一位都能够对后面的加密过程产生影响，提高加密强度

我们将把64位的顺序按下表中规定的顺序放置，图中的数字是在64位明文中每个比特的索引位置

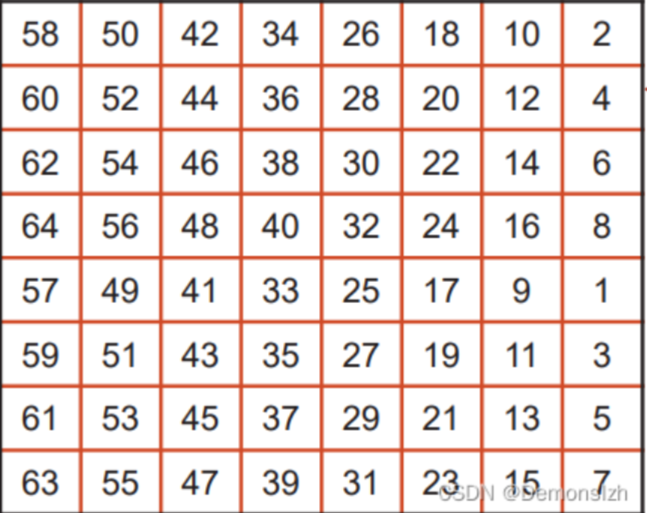
加密轮次

初始置换完成后，明文被划分成了相同长度（32位）的左右两部分，记作L0,R0。接下来就会进行16个轮次的加密

从单独一个轮次来看，首先把目光聚焦在R0这里。右半部分R0会作为下一轮次的左半部分L1的输入。其次，R0会补位到48位和本轮次生成的48位K0输入到F轮函数中去。F函数的输出结果为32位，结果F(R0,K0)会和L0进行异或运算作为下一轮次右半部分R1的输入

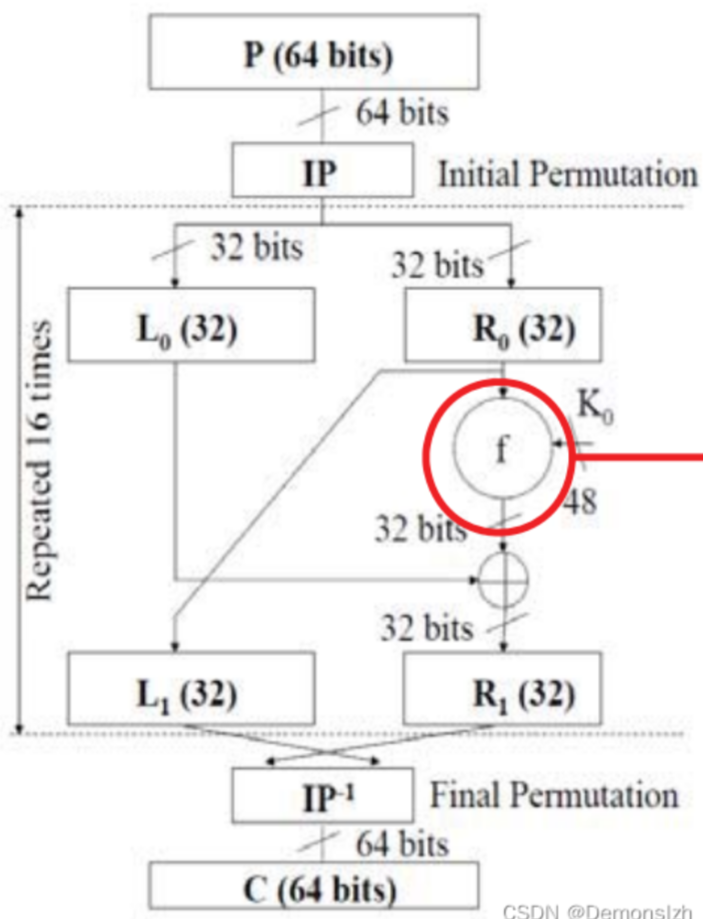
以此类推，重复16轮运算

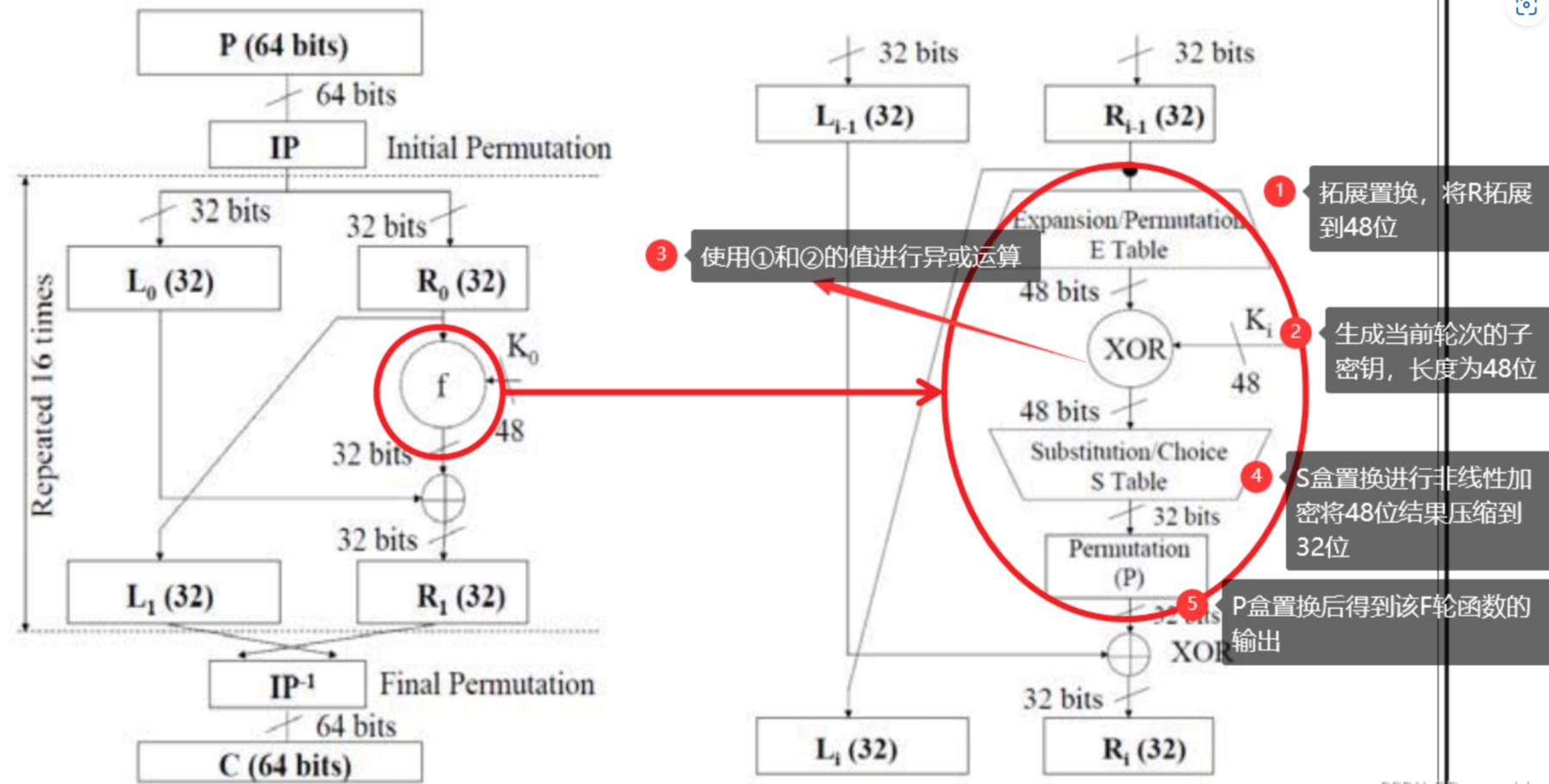
拓展R到48位

将32位的R0右半部分进行扩展，得到一个48位的数据块。同样的，数据拓展也是根据一个固定的置换表。红框中就是我们要补位的数据

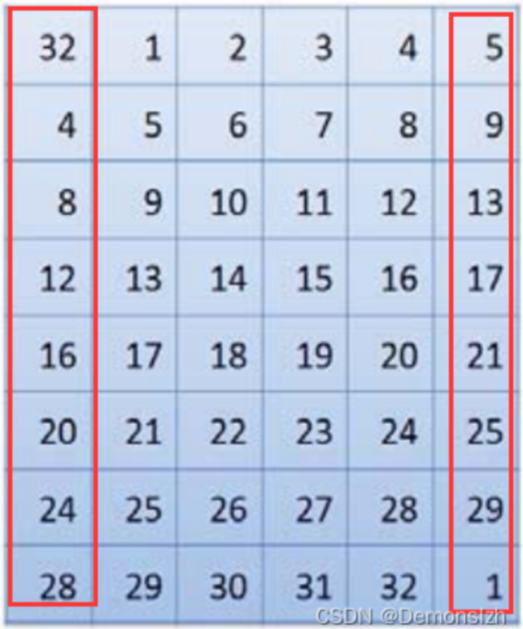
由此可见，扩展过程的每一位都是根据上述的置换表从输入的32位数据块中提取出来的。原始数据的第32位被补充到了新增列的第一个，第5位被补充到了第二个新增列的第一个，以此类推

子密钥k的生成

DES算法采用了每轮子密钥生成的方式来增加密钥的复杂性和安全性。每轮子密钥都是由主密钥（64位）通过密钥调度算法（Key Schedule Algorithm）生成的。DES算法的密钥调度算法可以将64位的主密钥分成16个子密钥，每个子密钥48位，用于每轮加密中与输入数据进行异或运算

通过子密钥生成的流程图来看下整个过程

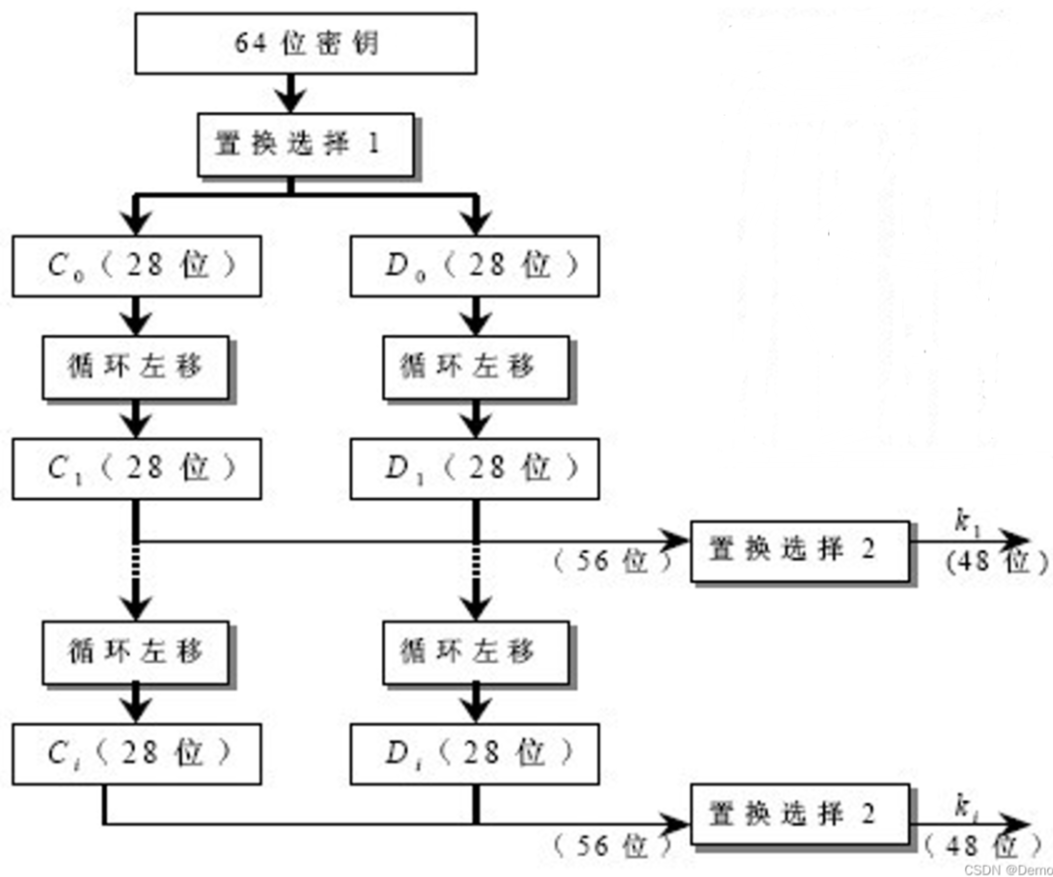
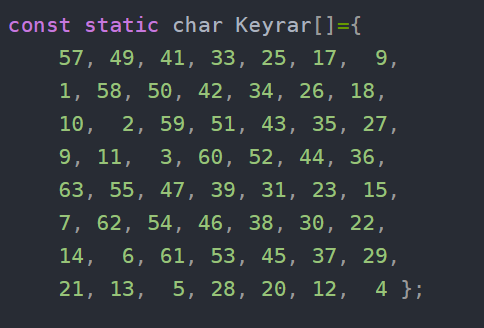
主密钥，下面56位是已经删除以8为倍数的奇偶校验位

异或

当前轮次的子密钥Ki（在上面56位的基础上删除特定的8位，得到48位）与拓展的48位Ri进行异或运算。运算结果会作为接下来S盒替换的输入

S盒替换

用于将上一轮异或运算的48位结果映射到32位输出中去

6位变4位，首尾两位作为行标，中间四位作为列标，去不同的S盒对应一个小于16的数，再转化为4位二进制数

P盒代换

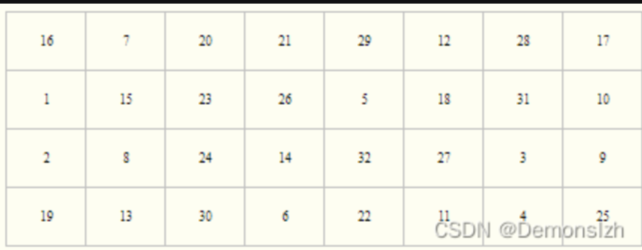
P盒代换将S盒替换的32位输出作为输入，经过上述固定的代换表进行代换后即为最后F轮函数的结果

逆置换

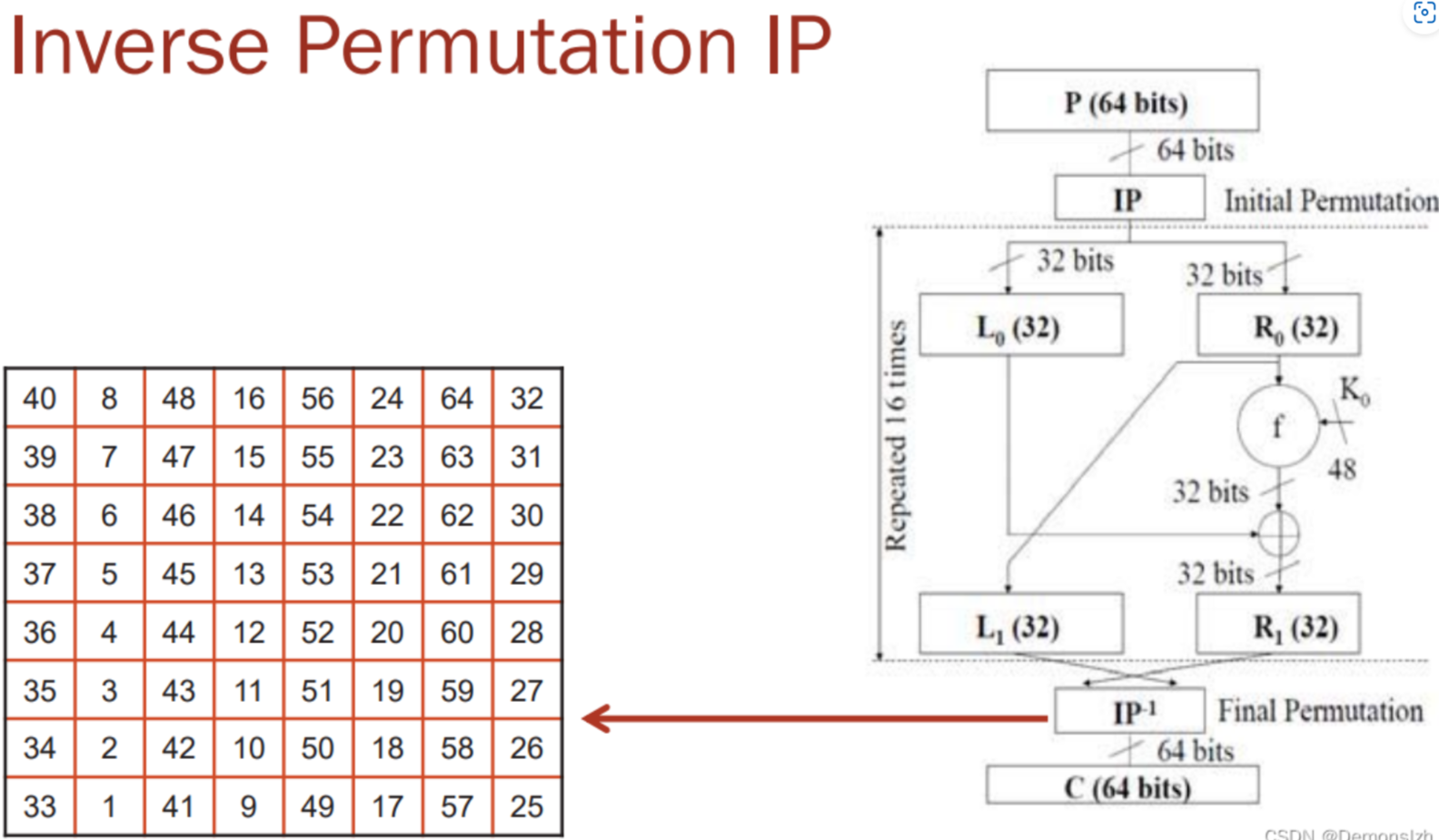
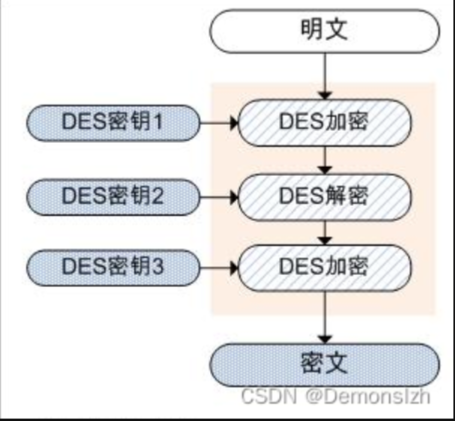
3DES

3DES顾名思义，就i是使用DES加密3次，使用3个密钥进行加解密

SM4

常数0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc

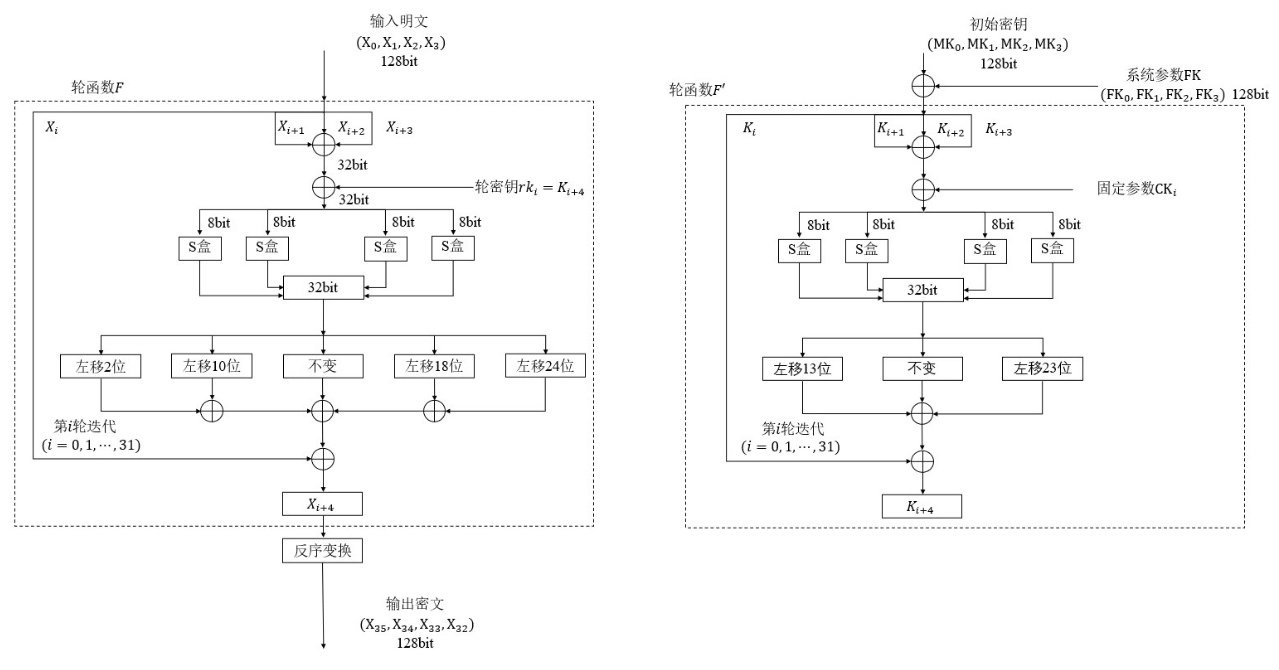
分组密码，分组长度128位，密钥长度128位，32轮迭代和一次反序变换，输入4字（16字节，换算方法是密码算法特有的）

分为密钥拓展和加/解密两个模块，下图是 SM4 的加解密（左）和密钥拓展（右）的流程图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
public class SM4 {
    int[] key_r;

    /* 初始化轮密钥 */
    SM4(byte[] key) {
        this.key_r = keyGenerate(key);
    }

    /* 密钥拓展 */
    private int[] keyGenerate(byte[] key) {
        int[] key_r = new int[32];//轮密钥rk_i
        int[] key_temp = new int[4];
        int box_in, box_out;//盒变换输入输出
        final int[] FK = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc};
        final int[] CK = {
                0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
                0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
                0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
                0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
                0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
                0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
                0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
                0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
        };
        //将输入的密钥每32比特合并，并异或FK
        for (int i = 0; i < 4; i++) {
            key_temp[i] = jointBytes(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
            key_temp[i] = key_temp[i] ^ FK[i];
        }
        //32轮密钥拓展
        for (int i = 0; i < 32; i++) {
            box_in = key_temp[1] ^ key_temp[2] ^ key_temp[3] ^ CK[i];
            box_out = sBox(box_in);
            key_r[i] = key_temp[0] ^ box_out ^ shift(box_out, 13) ^ shift(box_out, 23);
            key_temp[0] = key_temp[1];
            key_temp[1] = key_temp[2];
            key_temp[2] = key_temp[3];
            key_temp[3] = key_r[i];
        }
        return key_r;
    }

    
    private static byte[] sm4Main(byte[] input, int[] key_r, int mod) {
        int[] text = new int[4];//32比特字
        //将输入以32比特分组
        for (int i = 0; i < 4; i++) {
            text[i] = jointBytes(input[4 * i], input[4 * i + 1], input[4 * i + 2], input[4 * i + 3]);
        }
        int box_input, box_output;//盒变换输入和输出
        for (int i = 0; i < 32; i++) {
            int index = (mod == 0) ? i : (31 - i);//通过改变key_r的顺序改变模式
            box_input = text[1] ^ text[2] ^ text[3] ^ key_r[index];
            box_output = sBox(box_input);
            int temp = text[0] ^ box_output ^ shift(box_output, 2) ^ shift(box_output, 10) ^ shift(box_output, 18) ^ shift(box_output, 24);
            text[0] = text[1];
            text[1] = text[2];
            text[2] = text[3];
            text[3] = temp;
        }
        byte[] output = new byte[16];
        //将结果的32比特字拆分
        for (int i = 0; i < 4; i++) {
            System.arraycopy(splitInt(text[3 - i]), 0, output, 4 * i, 4);
        }
        return output;
    }

    
    public byte[] encrypt(byte[] plaintext) {
        return sm4Main(plaintext, key_r, 0);
    }

   
    public byte[] decrypt(byte[] ciphertext) {
        return sm4Main(ciphertext, key_r, 1);
    }

    /* 将32比特数拆分成4个8比特数 */
    private static byte[] splitInt(int n) {
        return new byte[]{(byte) (n >>> 24), (byte) (n >>> 16), (byte) (n >>> 8), (byte) n};
    }

    /* 将4个8比特数合并成32比特数 */
    private static int jointBytes(byte byte_0, byte byte_1, byte byte_2, byte byte_3) {
        return ((byte_0 & 0xFF) << 24) | ((byte_1 & 0xFF) << 16) | ((byte_2 & 0xFF) << 8) | (byte_3 & 0xFF);
    }
    
    /* S盒变换 */
    private static int sBox(int box_input) {
        
        final int[] SBOX = {
                0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05, 0x2B, 0x67, 0x9A,
                0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99, 0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF,
                0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62, 0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95, 0x80,
                0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6, 0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA, 0x83, 0x59, 0x3C, 0x19,
                0xE6, 0x85, 0x4F, 0xA8, 0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D,
                0x35, 0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87, 0xD4, 0x00,
                0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E, 0xEA, 0xBF, 0x8A, 0xD2, 0x40,
                0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1, 0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55,
                0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3, 0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23,
                0xAB, 0x0D, 0x53, 0x4E, 0x6F, 0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C,
                0x5B, 0x51, 0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8, 0x0A,
                0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD, 0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0, 0x89, 0x69, 0x97, 0x4A,
                0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84, 0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D,
                0x20, 0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48
        };

        byte[] temp = splitInt(box_input);//拆分32比特数
        byte[] output = new byte[4];//单个盒变换输出
        //盒变换
        for (int i = 0; i < 4; i++) {
            output[i] = (byte) SBOX[temp[i] & 0xFF];
        }
        //将4个8位字节合并为一个字作为盒变换输出
        return jointBytes(output[0], output[1], output[2], output[3]);
    }

    /* 将input左移n位 */
    private static int shift(int input, int n) {
        return (input >>> (32 - n)) | (input << n);
    }
}

加解密代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# -*- coding: utf-8 -*-

import binascii
from gmssl import sm4


class SM4:


    def __init__(self):
        self.crypt_sm4 = sm4.CryptSM4()  # 实例化

    def str_to_hexStr(self , hex_str):
        """
        字符串转hex
        :param hex_str: 字符串
        :return: hex
        """
        hex_data = hex_str.encode('utf-8')
        str_bin = binascii.unhexlify(hex_data)
        return str_bin.decode('utf-8')

    def encryptSM4(self , encrypt_key , value):
        """
        国密sm4加密
        :param encrypt_key: sm4加密key
        :param value: 待加密的字符串
        :return: sm4加密后的十六进制值
        """
        crypt_sm4 = self.crypt_sm4
        crypt_sm4.set_key(encrypt_key.encode() , sm4.SM4_ENCRYPT)  # 设置密钥
        date_str = str(value)
        encrypt_value = crypt_sm4.crypt_ecb(date_str.encode())  # 开始加密。bytes类型
        return encrypt_value.hex()  # 返回十六进制值

    def decryptSM4(self , decrypt_key , encrypt_value):
        """
        国密sm4解密
        :param decrypt_key:sm4加密key
        :param encrypt_value: 待解密的十六进制值
        :return: 原字符串
        """
        crypt_sm4 = self.crypt_sm4
        crypt_sm4.set_key(decrypt_key.encode() , sm4.SM4_DECRYPT)  # 设置密钥
        decrypt_value = crypt_sm4.crypt_ecb(bytes.fromhex(encrypt_value))  # 开始解密。十六进制类型
        return decrypt_value.decode()
        # return self.str_to_hexStr(decrypt_value.hex())


if __name__ == '__main__':
    key = "C3AE5873D08418DA"
    strData = '''{"addr":"","regnCode":"320100","medinsName":"","medinsLvCode":"","medinsTypeCode":"","openElec":"","pageNum":6,"pageSize":100}'''
    SM4 = SM4()
    print("原字符：" , strData)
    encData = SM4.encryptSM4(key , strData)  # 加密后的数据，返回bytes类型
    print("sm4加密结果：" , encData)

    decData = SM4.decryptSM4(key , encData)
    print("sm4解密结果：" , decData)  # 解密后的数据

MD5

[https://zhuanlan.zhihu.com/p/115270932#:~:text=C%E8%AF%AD%E8%A8%80%E5%AE%9E%E7%8E%B0%20%E4%BB%A5%E4%B8%8B%E4%BB%A3%E7%A0%81%E6%A0%B9%E6%8D%AE%E5%8F%82%E8%80%83%E6%96%87%E7%8C%AE%E4%BF%AE%E6%94%B9%E3%80%81%E6%B3%A8%E9%87%8A%E8%80%8C%E6%9D%A5%EF%BC%8C%E6%AF%95%E7%AB%9FMD5%E7%AE%97%E6%B3%95%E4%B8%8D%E6%98%AF%E6%88%91%E5%8E%9F%E5%88%9B%E7%9A%84%E3%80%82%20%2F%2A,%E5%87%BD%E6%95%B0%E4%BD%BF%E7%94%A8%E8%AF%B4%E6%98%8E%EF%BC%9A%20%E5%85%88%E8%B0%83%E7%94%A8MD5Init%E5%88%9D%E5%A7%8B%E5%8C%96%E4%B8%80%E4%B8%AAMD5_CTX%E7%B1%BB%E5%9E%8B%E7%BB%93%E6%9E%84%E4%BD%93%EF%BC%8C%E5%86%8D%E4%BD%BF%E7%94%A8MD5Update%E8%AE%A1%E7%AE%97MD5%E7%A0%81%EF%BC%8C%E6%9C%80%E5%90%8E%E8%B0%83%E7%94%A8MD5Final%E8%8E%B7%E5%8F%96%20%E4%BD%BF%E7%94%A8%E7%A4%BA%E4%BE%8B%E8%A7%81%E6%9C%80%E4%B8%8B%E9%9D%A2%E7%9A%84main%E5%87%BD%E6%95%B0%E3%80%82](https://zhuanlan.zhihu.com/p/115270932#:~:text=C语言实现 以下代码根据参考文献修改、注释而来，毕竟MD5算法不是我原创的。 %2F*,函数使用说明： 先调用MD5Init初始化一个MD5_CTX类型结构体，再使用MD5Update计算MD5码，最后调用MD5Final获取 使用示例见最下面的main函数。)

MD5加密的函数大致如下：

MD5_CTX md5c;（结构体）

MD5Init(&md5c);

MD5UpdateString(&md5c,plain)

MD5Final(digest,&md5c);

数据填充

MD5算法的第二步“分组循环变换”是以512位为一个分组进行处理的。因此，需要把数据填充成长度为512位的倍数。具体填充步骤如下：

1、先填充一个“1”，后面加上k个“0”。其中k是满足(n+1+k) mod 512 = 448的最小正整数。

2、追加64位的数据长度（bit为单位，小端序存放）

填充完的数据大概长这样：

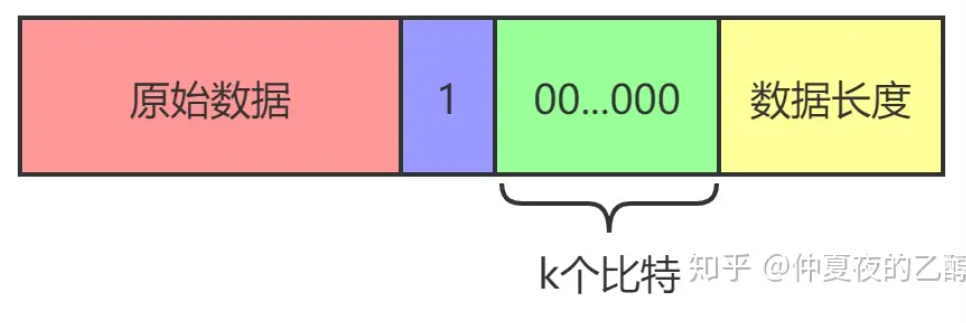
分组循环变换

其中，MD5Init会初始化四个称作MD5链接变量的整形参数。因此如果看到这4个常数0x67452301、0xefcdab89、0x98badcfe、0x10325476，就应该是MD5算法了。MD5Init函数代码如下：

1
2
3
4
5
6
7
8
9
10
void MD5Init(MD5_CTX *context)  
{  
     context->count[0] = 0;  
     context->count[1] = 0;  
     //Load magic initialization constants
     context->state[0] = 0x67452301;  
     context->state[1] = 0xEFCDAB89;  
     context->state[2] = 0x98BADCFE;  
     context->state[3] = 0x10325476;  
}

十进制表示如下，int最大是0x7fffffff，所以第2个和第3个为负数

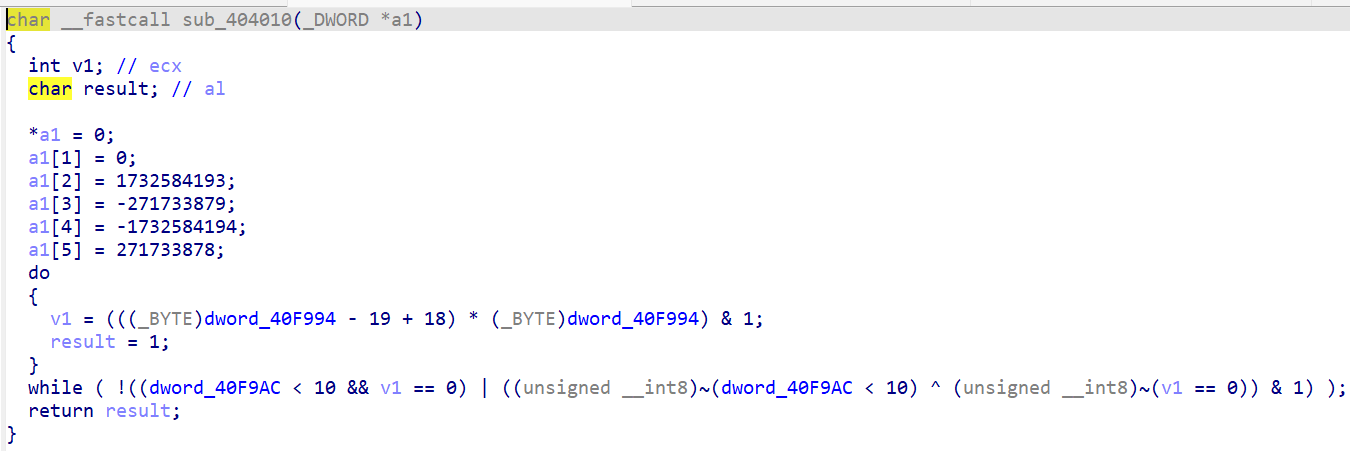
然后将填充完成后的数据划分成一个个512位的分组，依次进入循环变换。A、B、C、D也参与到循环变换中。数据分组进去变换的时候，大概走这么个流程：

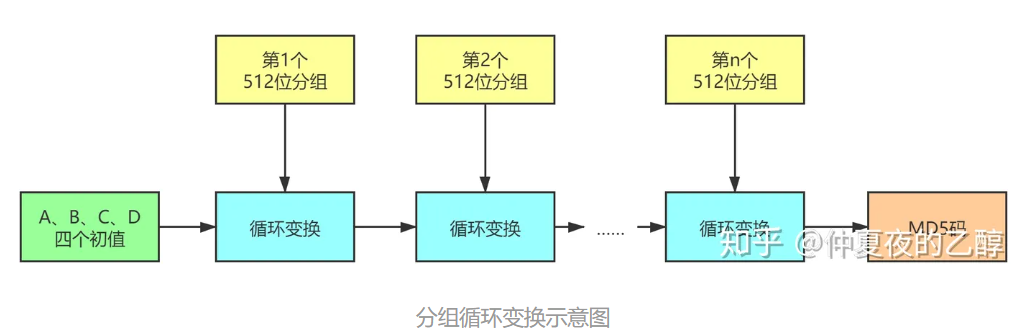
循环变换是整个MD5算法最核心，也是最复杂的部分。一个512位分组的数据被进一步划分为16个32位的子分组，对每个子分组进行下图所示的变换：

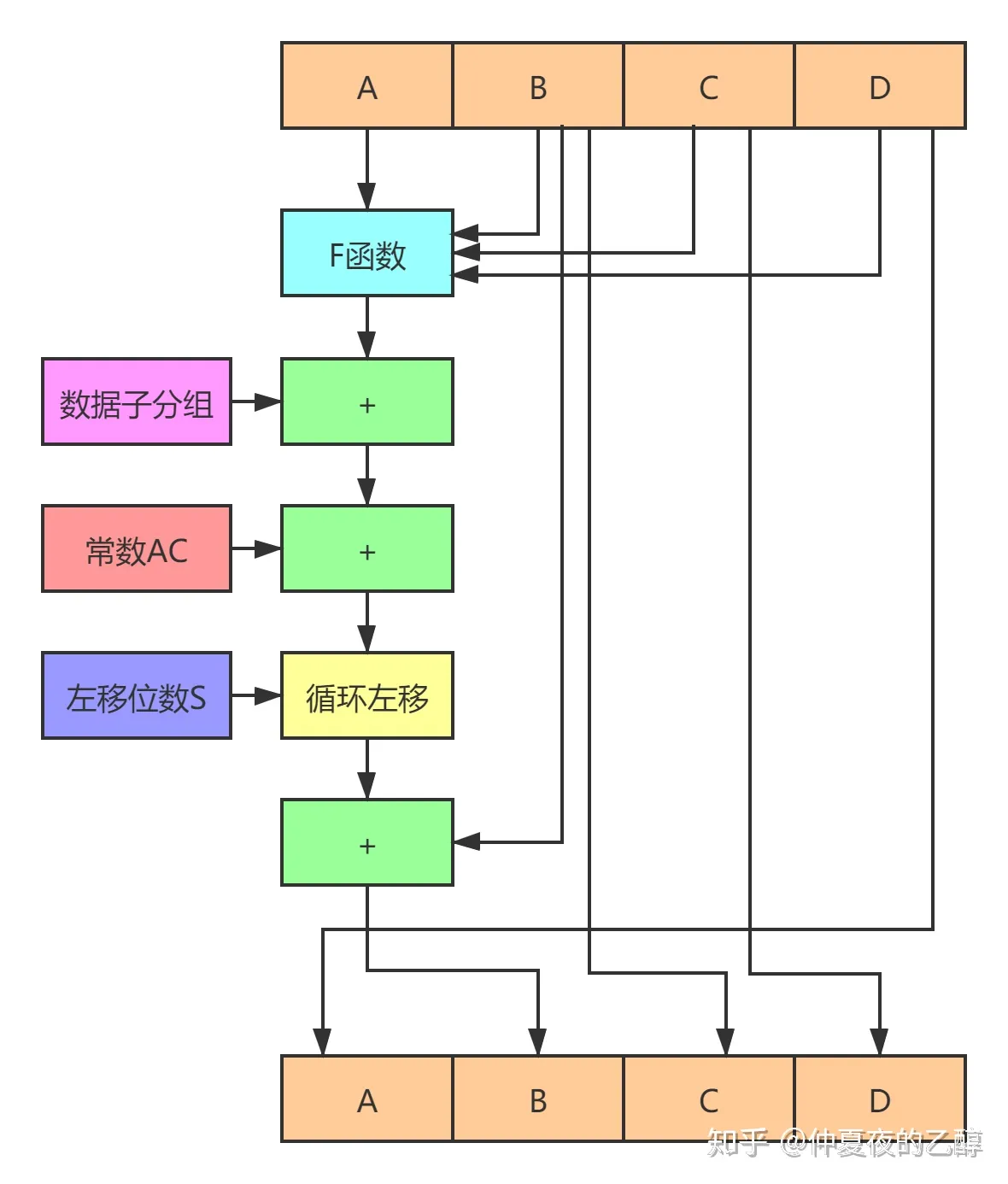
上面只是画出了一个子分组进行的变换。下面对图中的元素进行说明：

1.图中的F函数代表一次由位运算构成的非线性变换，每一轮循环变换用到的F函数不一样

2.常数AC的值在每一次变换中都不一样

3.左移位数S有规律地周期性变化

数据的16个子分组都参与到上图所示的变换，顺序不定。当16个子分组处理完成时，我们就说完成了一轮循环变换。MD5的一个数据分组一共需要进行四轮的循环变换。将四轮循环变换后得到的A、B、C、D的值分别和原来的值相加，就是A、B、C、D进行循环变换后的结果

拼接输出

将经过若干次循环变换后的A、B、C、D以十六进制的形式拼接起来，就是MD5码

这里是加密函数，而且也能看到hash[]

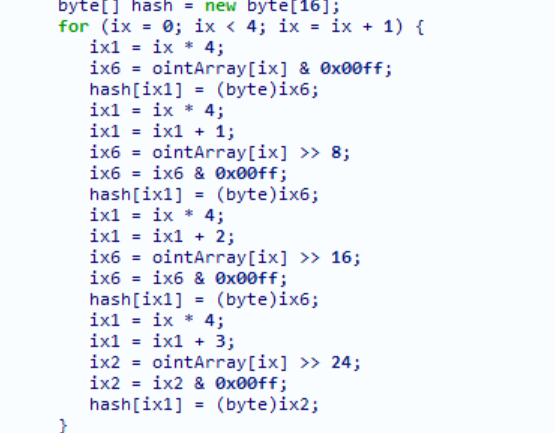
还有可能的特征

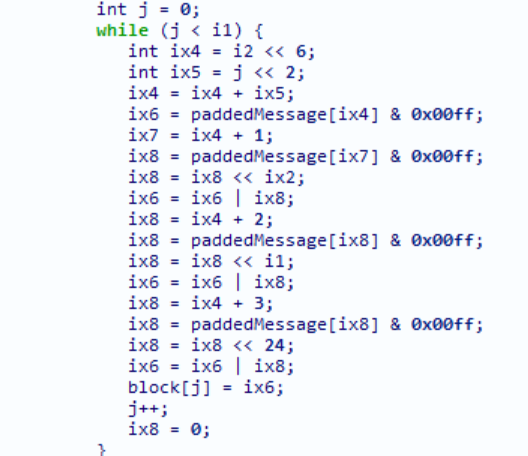
完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
/*
函数使用说明：
先调用MD5Init初始化一个MD5_CTX类型结构体，再使用MD5Update计算MD5码，最后调用MD5Final获取
*/

#include<string.h>
#include<stdio.h>
typedef unsigned char *POINTER; 
typedef struct {
    unsigned int state[4];                                   /* A,B,C,D四个常数 */
    unsigned int count[2];        /* 数据的bit数计数器(对2^64取余) */
    unsigned char buffer[64];                         /* 输入数据缓冲区 */
} MD5_CTX; //存放MD5算法相关信息的结构体定义

void MD5Init (MD5_CTX *);
void MD5Update(MD5_CTX *, unsigned char *, unsigned int);
void MD5Final(unsigned char [16], MD5_CTX *);
void MD5Transform(unsigned int [4], unsigned char [64]);
void Encode(unsigned char *, unsigned int *, unsigned int);
void Decode(unsigned int *, unsigned char *, unsigned int);

//循环左移的位数
#define S11 7
#define S12 12
#define S13 17
#define S14 22
#define S21 5
#define S22 9
#define S23 14
#define S24 20
#define S31 4
#define S32 11
#define S33 16
#define S34 23
#define S41 6
#define S42 10
#define S43 15
#define S44 21

//数据填充的内容
unsigned char PADDING[64] = {
    0x80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
    };

//F,G,H,I四个非线性变换函数
#define F(x, y, z) (((x) & (y)) | ((~x) & (z)))
#define G(x, y, z) (((x) & (z)) | ((y) & (~z)))
#define H(x, y, z) ((x) ^ (y) ^ (z))
#define I(x, y, z) ((y) ^ ((x) | (~z)))

//x循环左移n位的操作
#define ROTATE_LEFT(x, n) (((x) << (n)) | ((x) >> (32-(n))))

//FF,GG,HH,II是四轮循环变换分别用到的变换函数
#define FF(a, b, c, d, x, s, ac) { \
 (a) += F ((b), (c), (d)) + (x) + (unsigned int)(ac); \
 (a) = ROTATE_LEFT ((a), (s)); \
 (a) += (b); \
  }
#define GG(a, b, c, d, x, s, ac) { \
 (a) += G ((b), (c), (d)) + (x) + (unsigned int)(ac); \
 (a) = ROTATE_LEFT ((a), (s)); \
 (a) += (b); \
  }
#define HH(a, b, c, d, x, s, ac) { \
 (a) += H ((b), (c), (d)) + (x) + (unsigned int)(ac); \
 (a) = ROTATE_LEFT ((a), (s)); \
 (a) += (b); \
  }
#define II(a, b, c, d, x, s, ac) { \
 (a) += I ((b), (c), (d)) + (x) + (unsigned int)(ac); \
 (a) = ROTATE_LEFT ((a), (s)); \
 (a) += (b); \
  }


void MD5Init (MD5_CTX *context)
{
    //bit计数器清零
    context->count[0] = context->count[1] = 0;
    //A,B,C,D被初始化为四个特定的常数(Magic Number)
    context->state[0] = 0x67452301;
    context->state[1] = 0xefcdab89;
    context->state[2] = 0x98badcfe;
    context->state[3] = 0x10325476;
}

//使用MD5算法对input的数据进行处理
void MD5Update (MD5_CTX *context, unsigned char *input, unsigned int inputLen)
{
    unsigned int i, index, partLen;
    //计算[已处理数据长度(byte) mod 64]
    index = (unsigned int)((context->count[0] >> 3) & 0x3F);
    //bit计数器累加
    if ((context->count[0] += ((unsigned int)inputLen << 3))
      < ((unsigned int)inputLen << 3)) //处理加法进位溢出的情况
        context->count[1]++;
    context->count[1] += ((unsigned int)inputLen >> 29);
    //计算缓冲区还有多少字节空间
    partLen = 64 - index;
    //以512位数据为一组进行处理
    if (inputLen >= partLen) {
        memcpy(&context->buffer[index],input, partLen);
        MD5Transform (context->state, context->buffer);
        for (i = partLen; i + 63 < inputLen; i += 64)
            MD5Transform (context->state, &input[i]);
        index = 0;
    }
    else i = 0;
    //缓存未处理的输入
    memcpy(&context->buffer[index],&input[i],inputLen-i);
}

//获取MD5码（由digest返回），顺便清除context数据
void MD5Final (unsigned char digest[16], MD5_CTX *context)
{
    unsigned char bits[8];
    unsigned int index, padLen;
    //记录数据长度
    Encode (bits, context->count, 8);
    //填充数据
    index = (unsigned int)((context->count[0] >> 3) & 0x3f);
    padLen = (index < 56) ? (56 - index) : (120 - index);
    MD5Update (context, PADDING, padLen);
    //追加数据长度信息
    MD5Update (context, bits, 8);
    //获取MD5码。其实就是将ABCD四个32位整数以16进制方式级联
    Encode (digest, context->state, 16);
    //清除数据
    memset(context, 0, sizeof(*context));
}

//MD5变换函数
void MD5Transform (unsigned int state[4], unsigned char block[64])
{
    unsigned int a = state[0], b = state[1], c = state[2], d = state[3], x[16];
    //将64字节的一组数据进一步划分为16个子分组
    Decode (x, block, 64);
    //第1轮循环变换
    FF (a, b, c, d, x[ 0], S11, 0xd76aa478); /* 1 */
    FF (d, a, b, c, x[ 1], S12, 0xe8c7b756); /* 2 */
    FF (c, d, a, b, x[ 2], S13, 0x242070db); /* 3 */
    FF (b, c, d, a, x[ 3], S14, 0xc1bdceee); /* 4 */
    FF (a, b, c, d, x[ 4], S11, 0xf57c0faf); /* 5 */
    FF (d, a, b, c, x[ 5], S12, 0x4787c62a); /* 6 */
    FF (c, d, a, b, x[ 6], S13, 0xa8304613); /* 7 */
    FF (b, c, d, a, x[ 7], S14, 0xfd469501); /* 8 */
    FF (a, b, c, d, x[ 8], S11, 0x698098d8); /* 9 */
    FF (d, a, b, c, x[ 9], S12, 0x8b44f7af); /* 10 */
    FF (c, d, a, b, x[10], S13, 0xffff5bb1); /* 11 */
    FF (b, c, d, a, x[11], S14, 0x895cd7be); /* 12 */
    FF (a, b, c, d, x[12], S11, 0x6b901122); /* 13 */
    FF (d, a, b, c, x[13], S12, 0xfd987193); /* 14 */
    FF (c, d, a, b, x[14], S13, 0xa679438e); /* 15 */
    FF (b, c, d, a, x[15], S14, 0x49b40821); /* 16 */
    //第2轮循环变换
    GG (a, b, c, d, x[ 1], S21, 0xf61e2562); /* 17 */
    GG (d, a, b, c, x[ 6], S22, 0xc040b340); /* 18 */
    GG (c, d, a, b, x[11], S23, 0x265e5a51); /* 19 */
    GG (b, c, d, a, x[ 0], S24, 0xe9b6c7aa); /* 20 */
    GG (a, b, c, d, x[ 5], S21, 0xd62f105d); /* 21 */
    GG (d, a, b, c, x[10], S22,  0x2441453); /* 22 */
    GG (c, d, a, b, x[15], S23, 0xd8a1e681); /* 23 */
    GG (b, c, d, a, x[ 4], S24, 0xe7d3fbc8); /* 24 */
    GG (a, b, c, d, x[ 9], S21, 0x21e1cde6); /* 25 */
    GG (d, a, b, c, x[14], S22, 0xc33707d6); /* 26 */
    GG (c, d, a, b, x[ 3], S23, 0xf4d50d87); /* 27 */
    GG (b, c, d, a, x[ 8], S24, 0x455a14ed); /* 28 */
    GG (a, b, c, d, x[13], S21, 0xa9e3e905); /* 29 */
    GG (d, a, b, c, x[ 2], S22, 0xfcefa3f8); /* 30 */
    GG (c, d, a, b, x[ 7], S23, 0x676f02d9); /* 31 */
    GG (b, c, d, a, x[12], S24, 0x8d2a4c8a); /* 32 */
    //第3轮循环变换
    HH (a, b, c, d, x[ 5], S31, 0xfffa3942); /* 33 */
    HH (d, a, b, c, x[ 8], S32, 0x8771f681); /* 34 */
    HH (c, d, a, b, x[11], S33, 0x6d9d6122); /* 35 */
    HH (b, c, d, a, x[14], S34, 0xfde5380c); /* 36 */
    HH (a, b, c, d, x[ 1], S31, 0xa4beea44); /* 37 */
    HH (d, a, b, c, x[ 4], S32, 0x4bdecfa9); /* 38 */
    HH (c, d, a, b, x[ 7], S33, 0xf6bb4b60); /* 39 */
    HH (b, c, d, a, x[10], S34, 0xbebfbc70); /* 40 */
    HH (a, b, c, d, x[13], S31, 0x289b7ec6); /* 41 */
    HH (d, a, b, c, x[ 0], S32, 0xeaa127fa); /* 42 */
    HH (c, d, a, b, x[ 3], S33, 0xd4ef3085); /* 43 */
    HH (b, c, d, a, x[ 6], S34,  0x4881d05); /* 44 */
    HH (a, b, c, d, x[ 9], S31, 0xd9d4d039); /* 45 */
    HH (d, a, b, c, x[12], S32, 0xe6db99e5); /* 46 */
    HH (c, d, a, b, x[15], S33, 0x1fa27cf8); /* 47 */
    HH (b, c, d, a, x[ 2], S34, 0xc4ac5665); /* 48 */
    //第4轮循环变换
    II (a, b, c, d, x[ 0], S41, 0xf4292244); /* 49 */
    II (d, a, b, c, x[ 7], S42, 0x432aff97); /* 50 */
    II (c, d, a, b, x[14], S43, 0xab9423a7); /* 51 */
    II (b, c, d, a, x[ 5], S44, 0xfc93a039); /* 52 */
    II (a, b, c, d, x[12], S41, 0x655b59c3); /* 53 */
    II (d, a, b, c, x[ 3], S42, 0x8f0ccc92); /* 54 */
    II (c, d, a, b, x[10], S43, 0xffeff47d); /* 55 */
    II (b, c, d, a, x[ 1], S44, 0x85845dd1); /* 56 */
    II (a, b, c, d, x[ 8], S41, 0x6fa87e4f); /* 57 */
    II (d, a, b, c, x[15], S42, 0xfe2ce6e0); /* 58 */
    II (c, d, a, b, x[ 6], S43, 0xa3014314); /* 59 */
    II (b, c, d, a, x[13], S44, 0x4e0811a1); /* 60 */
    II (a, b, c, d, x[ 4], S41, 0xf7537e82); /* 61 */
    II (d, a, b, c, x[11], S42, 0xbd3af235); /* 62 */
    II (c, d, a, b, x[ 2], S43, 0x2ad7d2bb); /* 63 */
    II (b, c, d, a, x[ 9], S44, 0xeb86d391); /* 64 */

    state[0] += a;
    state[1] += b;
    state[2] += c;
    state[3] += d;
}

//将无符号整数转为字节类型数组
void Encode (unsigned char *output, unsigned int *input,unsigned int len)
{
    unsigned int i, j;

    for (i = 0, j = 0; j < len; i++, j += 4) {
        output[j] = (unsigned char)(input[i] & 0xff);
        output[j+1] = (unsigned char)((input[i] >> 8) & 0xff);
        output[j+2] = (unsigned char)((input[i] >> 16) & 0xff);
        output[j+3] = (unsigned char)((input[i] >> 24) & 0xff);
    }
}

//将字节类型数组转为无符号整数
void Decode (unsigned int *output, unsigned char *input, unsigned int len)
{
    unsigned int i, j;

    for (i = 0, j = 0; j < len; i++, j += 4)
        output[i] = ((unsigned int)input[j]) | (((unsigned int)input[j+1]) << 8) |
        (((unsigned int)input[j+2]) << 16) | (((unsigned int)input[j+3]) << 24);
}

int main()
{
    MD5_CTX md5_calc;
    char c[]="abc";
    unsigned char md5[16];
    //演示计算字符串abc的MD5码
    MD5Init(&md5_calc);
    MD5Update(&md5_calc,(unsigned char *)c,strlen(c));
    MD5Final(md5,&md5_calc);
    //输出MD5码
    printf("字符串abc的MD5码为：");
    for(int i=0;i<16;i++) printf("%02x",md5[i]);
    printf("\n");
    return 0;
}

BlowFish

是对称加密，是用来替代DES算法出现的，是 将一个数 拆分为 左右各32位然后 左边进行 ^ key_pbox 当作下一次循环的右边。右边 则是 右边 ^ F(左边)下次当作循环的左边

常量

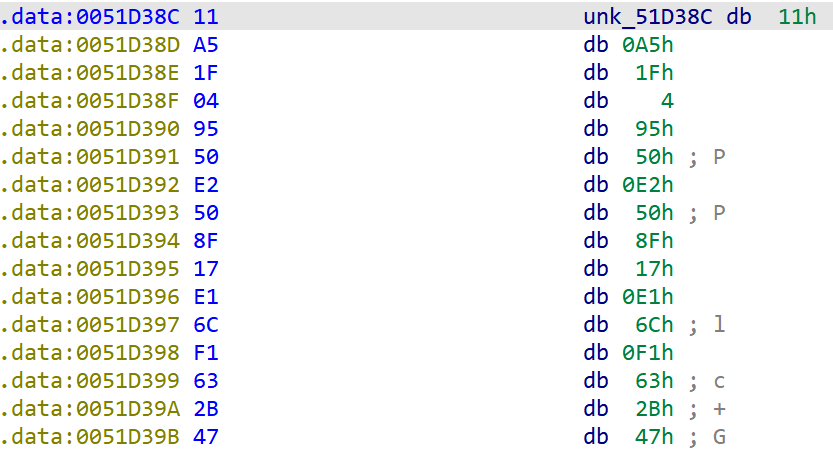
常见的前几位PBox

密钥扩展

循环轮数先是18，后是256

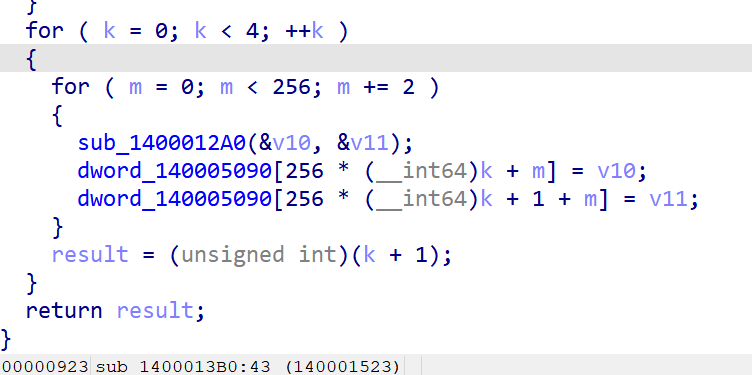
数据加密

16轮循环，里面有交换操作

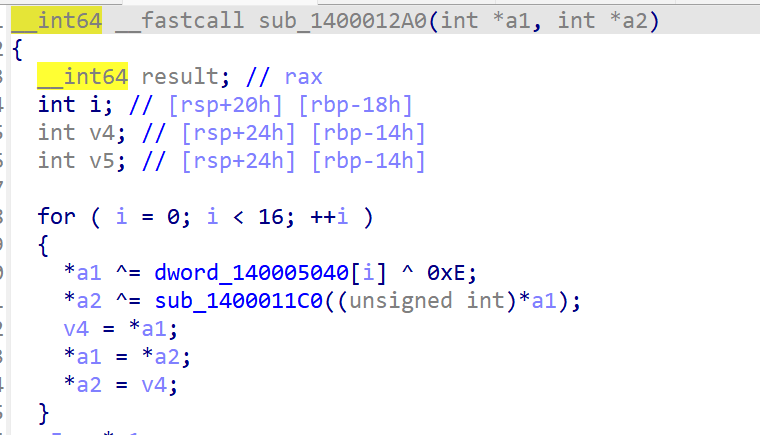
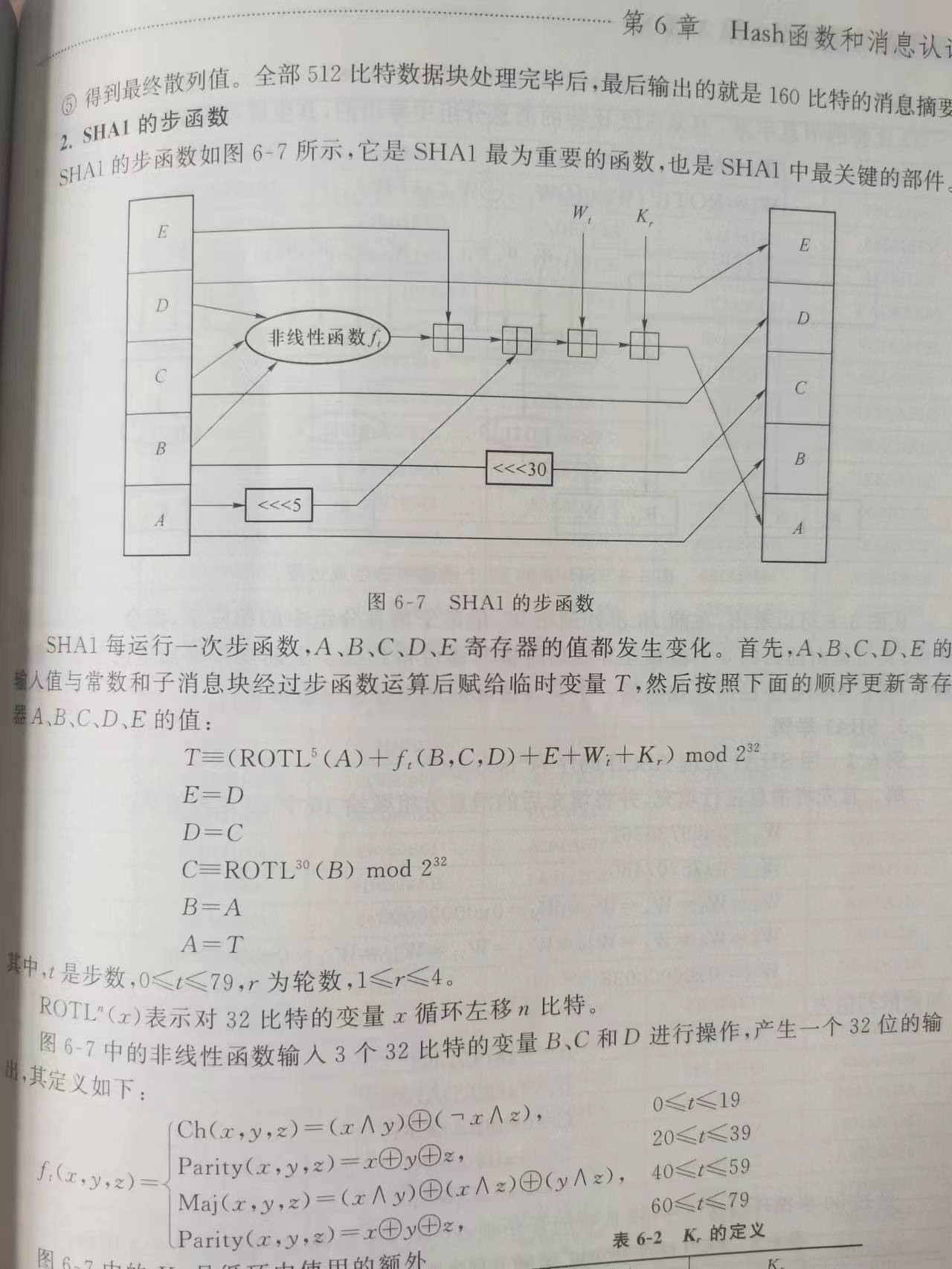
sha1

主循环4轮，每轮20次操作

有两组常量，分别对应k数组和MD buffer

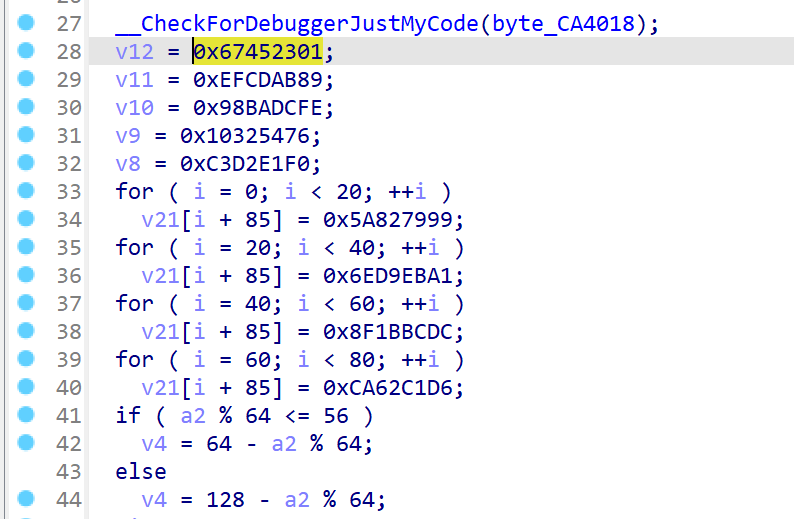
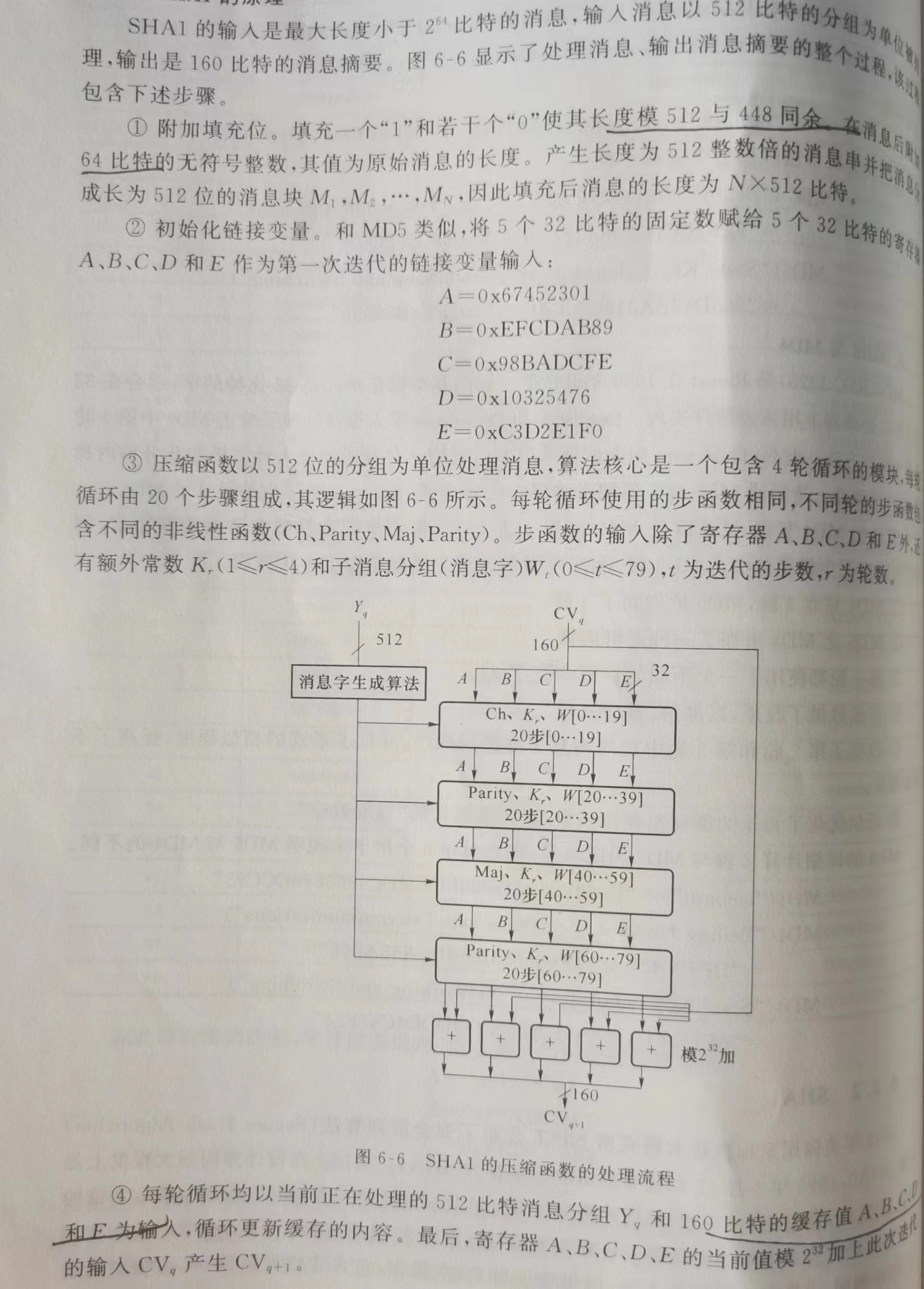
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
#include <string.h>
#include <stdio.h>
 
#define HASH_BLOCK_SIZE         64  /* 512 bits = 64 bytes */
#define HASH_LEN_SIZE           8   /* 64 bits =  8 bytes */
#define HASH_LEN_OFFSET         56  /* 64 bytes - 8 bytes */
#define HASH_DIGEST_SIZE        16  /* 128 bits = 16 bytes */
#define HASH_ROUND_NUM          80 
 
typedef unsigned char       uint8_t;
typedef unsigned short int  uint16_t;
typedef unsigned int        uint32_t;
typedef unsigned long long  uint64_t;
 
/* Swap bytes in 32 bit value. 0x01234567 -> 0x67452301 */
#define __bswap_32(x)    \
     ((((x) & 0xff000000) >> 24)  \
     | (((x) & 0x00ff0000) >>  8) \
     | (((x) & 0x0000ff00) <<  8) \
     | (((x) & 0x000000ff) << 24))
 
/* SHA1 Constants */
static uint32_t K[4] =
{
    0x5A827999,     /* [0,  19] */
    0x6ED9EBA1,     /* [20, 39] */
    0x8F1BBCDC,     /* [40, 59] */
    0xCA62C1D6      /* [60, 79] */
};
 
/*                  f(X, Y, Z)                      */
/* [0,  19] */
static uint32_t Ch(uint32_t X, uint32_t Y, uint32_t Z)
{
    return (X & Y) ^ ((~X) & Z);
}
/* [20, 39] */  /* [60, 79] */
static uint32_t Parity(uint32_t X, uint32_t Y, uint32_t Z)
{
    return X ^ Y ^ Z;
}
/* [40, 59] */
static uint32_t Maj(uint32_t X, uint32_t Y, uint32_t Z)
{
    return (X & Y) ^ (X & Z) ^ (Y & Z);
}
 
/* 循环向左移动offset个比特位 */
static uint32_t MoveLeft(uint32_t X, uint8_t offset)
{
    uint32_t res = (X << offset) | (X >> (32 - offset));
    return res;
}
 
#define ASSERT_RETURN_INT(x, d) if(!(x)) { return d; }
 
int sha1(unsigned char *out, const unsigned char* in, const int inlen)
{
    ASSERT_RETURN_INT(out && in && (inlen >= 0), 1);
    int i = 0, j = 0, t = 0;
 
    // step 1: 字节填充(Append Padding Bytes)
    // 数据先补上1个1比特，再补上k个0比特，使得补位后的数据比特数(n+1+k)满足(n+1+k) mod 512 = 448，k取最小正整数
    int iX = inlen / HASH_BLOCK_SIZE;
    int iY = inlen % HASH_BLOCK_SIZE;
    iX = (iY < HASH_LEN_OFFSET) ? iX : (iX + 1);
 
    int iLen = (iX + 1) * HASH_BLOCK_SIZE;
    unsigned char* X = malloc(iLen);
    memcpy(X, in, inlen);
    // 先补上1个1比特+7个0比特
    X[inlen] = 0x80;
    // 再补上(k-7)个0比特
    for (i = inlen + 1; i < (iX * HASH_BLOCK_SIZE + HASH_LEN_OFFSET); i++)
    {
        X[i] = 0;
    }
 
    // step 2: 追加长度信息(Append Length)
    uint8_t *pLen = (uint64_t*)(X + (iX * HASH_BLOCK_SIZE + HASH_LEN_OFFSET));
    uint64_t iTempLen = inlen << 3;
    uint8_t *pTempLen = &iTempLen;
    pLen[0] = pTempLen[7]; pLen[1] = pTempLen[6]; pLen[2] = pTempLen[5];  pLen[3] = pTempLen[4];
    pLen[4] = pTempLen[3]; pLen[5] = pTempLen[2]; pLen[6] = pTempLen[1];  pLen[7] = pTempLen[0];
 
    // Step 3. 初始化MD Buffer(Initialize MD Buffer)
    uint32_t H0 = 0x67452301;   // 0x01, 0x23, 0x45, 0x67
    uint32_t H1 = 0xEFCDAB89;   // 0x89, 0xAB, 0xCD, 0xEF
    uint32_t H2 = 0x98BADCFE;   // 0xFE, 0xDC, 0xBA, 0x98
    uint32_t H3 = 0x10325476;   // 0x76, 0x54, 0x32, 0x10
    uint32_t H4 = 0xC3D2E1F0;   // 0xF0, 0xE1, 0xD2, 0xC3
 
    uint32_t M[HASH_BLOCK_SIZE / 4] = { 0 };
    uint32_t W[HASH_ROUND_NUM] = { 0 };
 
    // step 4: 处理消息块(Process Message in 64-Byte Blocks)
    for (i = 0; i < iLen / HASH_BLOCK_SIZE; i++)
    {
        /* Copy block i into X. */
        for (j = 0; j < HASH_BLOCK_SIZE; j = j + 4)
        {
            uint64_t k = i * HASH_BLOCK_SIZE + j;
            M[j / 4] = (X[k] << 24) | (X[k + 1] << 16) | (X[k + 2] << 8) | X[k + 3];
        }
 
        /*  a. Divide M(i) into 16 words W(0), W(1), ..., W(15), where W(0) is the left - most word. */
        for (t = 0; t <= 15; t++)
        {
            W[t] = M[t];
        }
 
        /*  b. For t = 16 to 79 let
        W(t) = S^1(W(t-3) XOR W(t-8) XOR W(t-14) XOR W(t-16)). */
        for (t = 16; t <= 79; t++)
        {
            W[t] = MoveLeft(W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16], 1);
        }
 
        /*  c. Let A = H0, B = H1, C = H2, D = H3, E = H4. */
        uint32_t A = H0;
        uint32_t B = H1;
        uint32_t C = H2;
        uint32_t D = H3;
        uint32_t E = H4;
 
        /*  d. For t = 0 to 79 do
        TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);
        E = D;  D = C;  C = S^30(B);  B = A; A = TEMP; */
        for (t = 0; t <= 19; t++)
        {
            uint32_t temp = MoveLeft(A, 5) + Ch(B, C, D) + E + W[t] + K[0];
            E = D;
            D = C;
            C = MoveLeft(B, 30);
            B = A;
            A = temp;
        }
        for (t = 20; t <= 39; t++)
        {
            uint32_t temp = MoveLeft(A, 5) + Parity(B, C, D) + E + W[t] + K[1];
            E = D;
            D = C;
            C = MoveLeft(B, 30);
            B = A;
            A = temp;
        }
        for (t = 40; t <= 59; t++)
        {
            uint32_t temp = MoveLeft(A, 5) + Maj(B, C, D) + E + W[t] + K[2];
            E = D;
            D = C;
            C = MoveLeft(B, 30);
            B = A;
            A = temp;
        }
        for (t = 60; t <= 79; t++)
        {
            uint32_t temp = MoveLeft(A, 5) + Parity(B, C, D) + E + W[t] + K[3];
            E = D;
            D = C;
            C = MoveLeft(B, 30);
            B = A;
            A = temp;
        }
 
        /*  e. Let H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E. */
        H0 = H0 + A;
        H1 = H1 + B;
        H2 = H2 + C;
        H3 = H3 + D;
        H4 = H4 + E;
    }
 
    // step 5: 输出ABCD
    uint32_t* pOut = (uint8_t*)out;
    pOut[0] = __bswap_32(H0);
    pOut[1] = __bswap_32(H1);
    pOut[2] = __bswap_32(H2);
    pOut[3] = __bswap_32(H3);
    pOut[4] = __bswap_32(H4);
    free(X);
 
    return 0;
}
 
int main()
{
    unsigned char digest[20] = { 0 };
 
    sha1(digest, "Hello World!", strlen("Hello World!"));
 
    return 0;
}

祖冲之（ZUC)

序列密码，参考加解密脚本，需要已知key和iv

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
from math import ceil
 
S0 = [
    0x3E, 0x72, 0x5B, 0x47, 0xCA, 0xE0, 0x00, 0x33, 0x04, 0xD1, 0x54, 0x98, 0x09, 0xB9, 0x6D, 0xCB,
    0x7B, 0x1B, 0xF9, 0x32, 0xAF, 0x9D, 0x6A, 0xA5, 0xB8, 0x2D, 0xFC, 0x1D, 0x08, 0x53, 0x03, 0x90,
    0x4D, 0x4E, 0x84, 0x99, 0xE4, 0xCE, 0xD9, 0x91, 0xDD, 0xB6, 0x85, 0x48, 0x8B, 0x29, 0x6E, 0xAC,
    0xCD, 0xC1, 0xF8, 0x1E, 0x73, 0x43, 0x69, 0xC6, 0xB5, 0xBD, 0xFD, 0x39, 0x63, 0x20, 0xD4, 0x38,
    0x76, 0x7D, 0xB2, 0xA7, 0xCF, 0xED, 0x57, 0xC5, 0xF3, 0x2C, 0xBB, 0x14, 0x21, 0x06, 0x55, 0x9B,
    0xE3, 0xEF, 0x5E, 0x31, 0x4F, 0x7F, 0x5A, 0xA4, 0x0D, 0x82, 0x51, 0x49, 0x5F, 0xBA, 0x58, 0x1C,
    0x4A, 0x16, 0xD5, 0x17, 0xA8, 0x92, 0x24, 0x1F, 0x8C, 0xFF, 0xD8, 0xAE, 0x2E, 0x01, 0xD3, 0xAD,
    0x3B, 0x4B, 0xDA, 0x46, 0xEB, 0xC9, 0xDE, 0x9A, 0x8F, 0x87, 0xD7, 0x3A, 0x80, 0x6F, 0x2F, 0xC8,
    0xB1, 0xB4, 0x37, 0xF7, 0x0A, 0x22, 0x13, 0x28, 0x7C, 0xCC, 0x3C, 0x89, 0xC7, 0xC3, 0x96, 0x56,
    0x07, 0xBF, 0x7E, 0xF0, 0x0B, 0x2B, 0x97, 0x52, 0x35, 0x41, 0x79, 0x61, 0xA6, 0x4C, 0x10, 0xFE,
    0xBC, 0x26, 0x95, 0x88, 0x8A, 0xB0, 0xA3, 0xFB, 0xC0, 0x18, 0x94, 0xF2, 0xE1, 0xE5, 0xE9, 0x5D,
    0xD0, 0xDC, 0x11, 0x66, 0x64, 0x5C, 0xEC, 0x59, 0x42, 0x75, 0x12, 0xF5, 0x74, 0x9C, 0xAA, 0x23,
    0x0E, 0x86, 0xAB, 0xBE, 0x2A, 0x02, 0xE7, 0x67, 0xE6, 0x44, 0xA2, 0x6C, 0xC2, 0x93, 0x9F, 0xF1,
    0xF6, 0xFA, 0x36, 0xD2, 0x50, 0x68, 0x9E, 0x62, 0x71, 0x15, 0x3D, 0xD6, 0x40, 0xC4, 0xE2, 0x0F,
    0x8E, 0x83, 0x77, 0x6B, 0x25, 0x05, 0x3F, 0x0C, 0x30, 0xEA, 0x70, 0xB7, 0xA1, 0xE8, 0xA9, 0x65,
    0x8D, 0x27, 0x1A, 0xDB, 0x81, 0xB3, 0xA0, 0xF4, 0x45, 0x7A, 0x19, 0xDF, 0xEE, 0x78, 0x34, 0x60
]
 
S1 = [
    0x55, 0xC2, 0x63, 0x71, 0x3B, 0xC8, 0x47, 0x86, 0x9F, 0x3C, 0xDA, 0x5B, 0x29, 0xAA, 0xFD, 0x77,
    0x8C, 0xC5, 0x94, 0x0C, 0xA6, 0x1A, 0x13, 0x00, 0xE3, 0xA8, 0x16, 0x72, 0x40, 0xF9, 0xF8, 0x42,
    0x44, 0x26, 0x68, 0x96, 0x81, 0xD9, 0x45, 0x3E, 0x10, 0x76, 0xC6, 0xA7, 0x8B, 0x39, 0x43, 0xE1,
    0x3A, 0xB5, 0x56, 0x2A, 0xC0, 0x6D, 0xB3, 0x05, 0x22, 0x66, 0xBF, 0xDC, 0x0B, 0xFA, 0x62, 0x48,
    0xDD, 0x20, 0x11, 0x06, 0x36, 0xC9, 0xC1, 0xCF, 0xF6, 0x27, 0x52, 0xBB, 0x69, 0xF5, 0xD4, 0x87,
    0x7F, 0x84, 0x4C, 0xD2, 0x9C, 0x57, 0xA4, 0xBC, 0x4F, 0x9A, 0xDF, 0xFE, 0xD6, 0x8D, 0x7A, 0xEB,
    0x2B, 0x53, 0xD8, 0x5C, 0xA1, 0x14, 0x17, 0xFB, 0x23, 0xD5, 0x7D, 0x30, 0x67, 0x73, 0x08, 0x09,
    0xEE, 0xB7, 0x70, 0x3F, 0x61, 0xB2, 0x19, 0x8E, 0x4E, 0xE5, 0x4B, 0x93, 0x8F, 0x5D, 0xDB, 0xA9,
    0xAD, 0xF1, 0xAE, 0x2E, 0xCB, 0x0D, 0xFC, 0xF4, 0x2D, 0x46, 0x6E, 0x1D, 0x97, 0xE8, 0xD1, 0xE9,
    0x4D, 0x37, 0xA5, 0x75, 0x5E, 0x83, 0x9E, 0xAB, 0x82, 0x9D, 0xB9, 0x1C, 0xE0, 0xCD, 0x49, 0x89,
    0x01, 0xB6, 0xBD, 0x58, 0x24, 0xA2, 0x5F, 0x38, 0x78, 0x99, 0x15, 0x90, 0x50, 0xB8, 0x95, 0xE4,
    0xD0, 0x91, 0xC7, 0xCE, 0xED, 0x0F, 0xB4, 0x6F, 0xA0, 0xCC, 0xF0, 0x02, 0x4A, 0x79, 0xC3, 0xDE,
    0xA3, 0xEF, 0xEA, 0x51, 0xE6, 0x6B, 0x18, 0xEC, 0x1B, 0x2C, 0x80, 0xF7, 0x74, 0xE7, 0xFF, 0x21,
    0x5A, 0x6A, 0x54, 0x1E, 0x41, 0x31, 0x92, 0x35, 0xC4, 0x33, 0x07, 0x0A, 0xBA, 0x7E, 0x0E, 0x34,
    0x88, 0xB1, 0x98, 0x7C, 0xF3, 0x3D, 0x60, 0x6C, 0x7B, 0xCA, 0xD3, 0x1F, 0x32, 0x65, 0x04, 0x28,
    0x64, 0xBE, 0x85, 0x9B, 0x2F, 0x59, 0x8A, 0xD7, 0xB0, 0x25, 0xAC, 0xAF, 0x12, 0x03, 0xE2, 0xF2
]
 
D = [
    0x44D7, 0x26BC, 0x626B, 0x135E, 0x5789, 0x35E2, 0x7135, 0x09AF,
    0x4D78, 0x2F13, 0x6BC4, 0x1AF1, 0x5E26, 0x3C4D, 0x789A, 0x47AC
]
 
 
def addition_uint31(a, b):
    c = a + b
    return (c & 0x7FFFFFFF) + (c >> 31)
 
 
def rotl_uint31(a, shift):
    return ((a << shift) | (a >> (31 - shift))) & 0x7FFFFFFF
 
 
def rotl_uint32(a, shift):
    return ((a << shift) | (a >> (32 - shift))) & 0xFFFFFFFF
 
 
def l1(x):
    return (x ^ rotl_uint32(x, 2) ^ rotl_uint32(x, 10) ^ rotl_uint32(x, 18) ^ rotl_uint32(x, 24))
 
 
def l2(x):
    return (x ^ rotl_uint32(x, 8) ^ rotl_uint32(x, 14) ^ rotl_uint32(x, 22) ^ rotl_uint32(x, 30))
 
 
def make_uint32(a, b, c, d):
    return ((a << 24) & 0xffffffff) | ((b << 16) & 0xffffffff) | ((c << 8) & 0xffffffff) | d
 
 
def make_uint31(a, b, c):
    return ((a << 23) & 0x7fffffff) | ((b << 8) & 0x7fffffff) | c
 
 
class ZUC(object):
    def __init__(self, key, iv):
        self.r = [0, 0]
        self.lfsr = [0 for _ in range(16)]
        self.x = [0, 0, 0, 0]
        self.zuc_init(key, iv)
 
    def bit_reorganization(self):
        self.x[0] = ((self.lfsr[15] & 0x7FFF8000) << 1) | (self.lfsr[14] & 0xFFFF)
        self.x[1] = ((self.lfsr[11] & 0xFFFF) << 16) | (self.lfsr[9] >> 15)
        self.x[2] = ((self.lfsr[7] & 0xFFFF) << 16) | (self.lfsr[5] >> 15)
        self.x[3] = ((self.lfsr[2] & 0xFFFF) << 16) | (self.lfsr[0] >> 15)
 
    def lfsr_next(self):
        f = self.lfsr[0]
        v = rotl_uint31(self.lfsr[0], 8)
        f = addition_uint31(f, v)
        v = rotl_uint31(self.lfsr[4], 20)
        f = addition_uint31(f, v)
        v = rotl_uint31(self.lfsr[10], 21)
        f = addition_uint31(f, v)
        v = rotl_uint31(self.lfsr[13], 17)
        f = addition_uint31(f, v)
        v = rotl_uint31(self.lfsr[15], 15)
        f = addition_uint31(f, v)
        return f
 
    def lfsr_append(self, f):
        self.lfsr.append(f)
        if len(self.lfsr) > 16:
            self.lfsr.pop(0)
 
    def lfsr_init(self, u):
        self.lfsr_append(addition_uint31(self.lfsr_next(), u))
 
    def lfsr_shift(self):
        self.lfsr_append(self.lfsr_next())
 
    def f(self):
        W = ((self.x[0] ^ self.r[0]) + self.r[1]) & 0xffffffff
        W1 = (self.r[0] + self.x[1]) & 0xffffffff
        W2 = self.r[1] ^ self.x[2]
        u = l1(((W1 & 0x0000ffff) << 16) | (W2 >> 16))
        v = l2(((W2 & 0x0000ffff) << 16) | (W1 >> 16))
        self.r = [make_uint32(S0[u >> 24], S1[(u >> 16) & 0xFF],
                              S0[(u >> 8) & 0xFF], S1[u & 0xFF]),
                  make_uint32(S0[v >> 24], S1[(v >> 16) & 0xFF],
                              S0[(v >> 8) & 0xFF], S1[v & 0xFF])]
        return W
 
    def zuc_init(self, key, iv):
        # Expand key.
        self.lfsr = [make_uint31(key[i], D[i], iv[i]) for i in range(16)]
        self.r = [0, 0]
        for i in range(32):
            self.bit_reorganization()
            w = self.f()
            self.lfsr_init(w >> 1)
 
    def zuc_generate_keystream(self, length):
        keystream_buffer = []
        self.bit_reorganization()
        self.f()  # Discard the output of F.
 
        def itor():
            self.lfsr_shift()
            self.bit_reorganization()
            return self.f() ^ self.x[-1]
 
        keystream_buffer = [itor() for _ in range(length)]
        self.lfsr_shift()
        return keystream_buffer
 
    def zuc_encrypt(self, input):
        length = len(input)
        key_stream = self.zuc_generate_keystream(length)
        return [inp ^ key_stream[i] for i, inp in enumerate(input)]
 
 
if '__main__' == __name__:
    key = [0x00] * 16
    iv = [0x00] * 16
    zuc = ZUC(key, iv)
    # 加密过程
    out = zuc.zuc_encrypt(b"i love u")
    print("加密得到的字流", ["%08x" % e for e in out])
    # 解密过程
    zuc2 = ZUC(key, iv)
    out2 = zuc2.zuc_encrypt(out)
    print("解密得到的字流", ["%08x" % e for e in out2])
    print(bytes(out2))

base58

基本思想：常⽤的字节码（256进制）转换成Base58，相当于将256进制转换成58进制

经典脚本，表的长度是61，1-9+大小写字母，一般会多次出现58

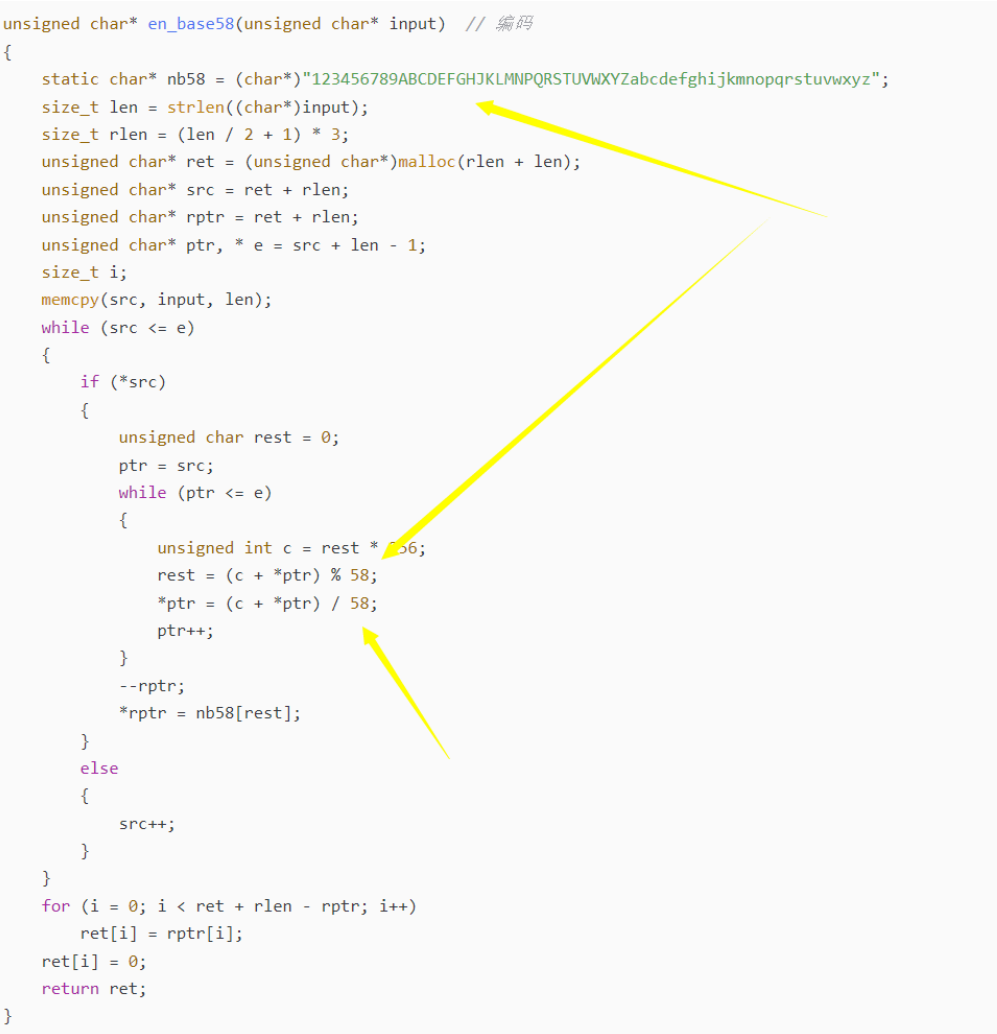
也有这样的

编码过程是：

\1. 将要转换的数据转换为字节数组

\2. 计算前置字节码是0的个数，因为0没必要参与转换，其结果是0。

\3. 将256进制转换为10进制

\4. 将10进制转换为58进制。

\5. 得到⼀个58进制的数组，将第⼆步0的个数添加到该数组末尾。n个0就添加n个0到数组末尾。

\6. 反转整个数组。

\7. 查表，将base58编码转换成字符。

这⾥的第3步如果转换的字节数组很⻓，那么以256为底数的指数将会⾮常庞⼤，需要使⽤⼤数，但实际上可以优化算法，没必要⼀次性将整个原始数组全部转换为10进制后才转换为58进制，可采取逐个转换为58进制的策略来进⾏，这样可以避免使⽤⼤整数，从⽽提⾼运算效率。

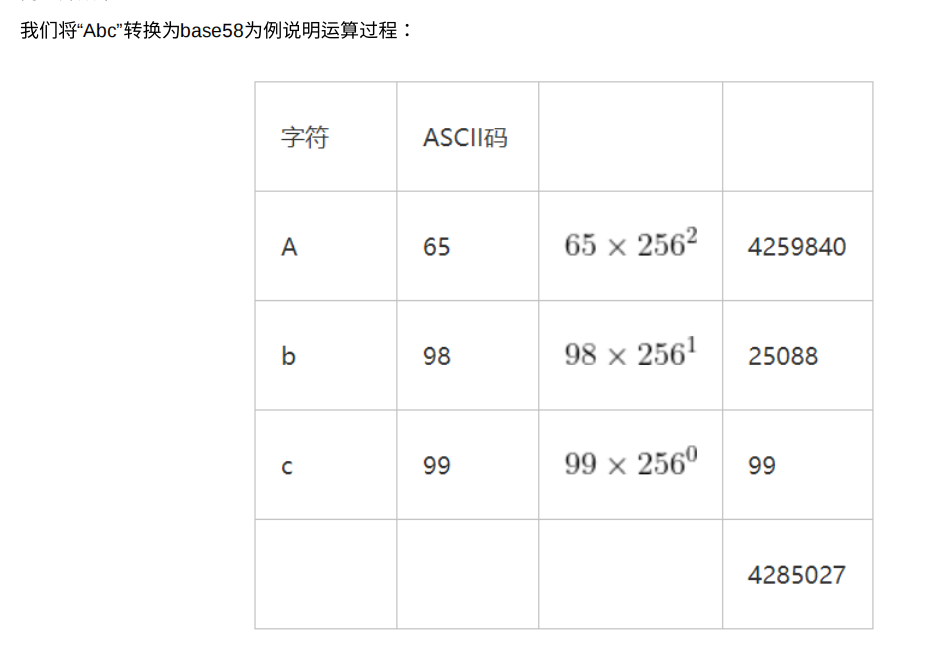
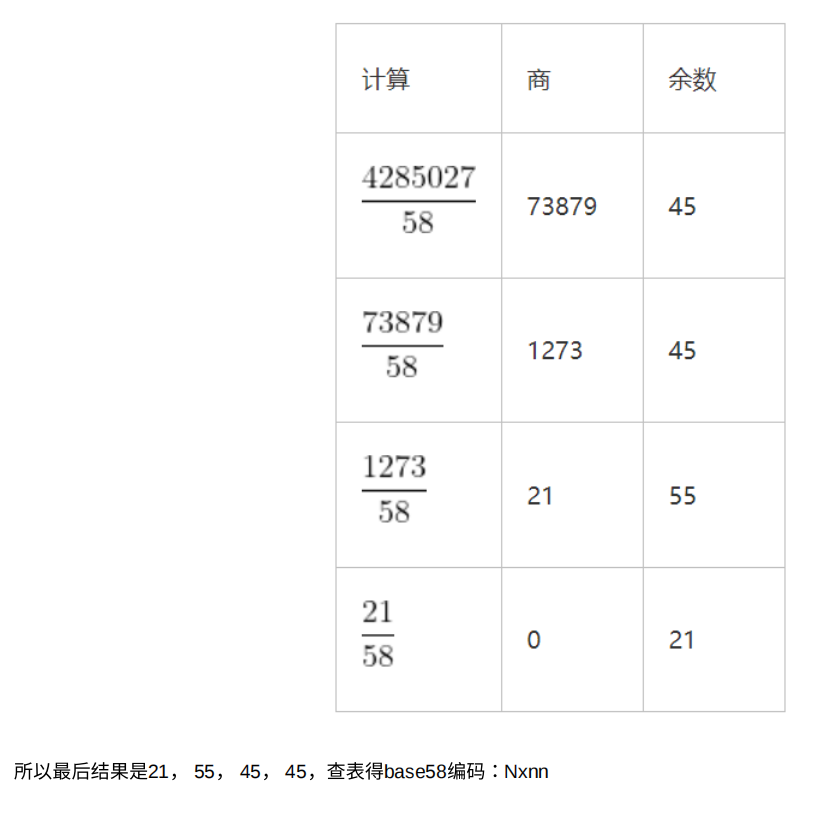
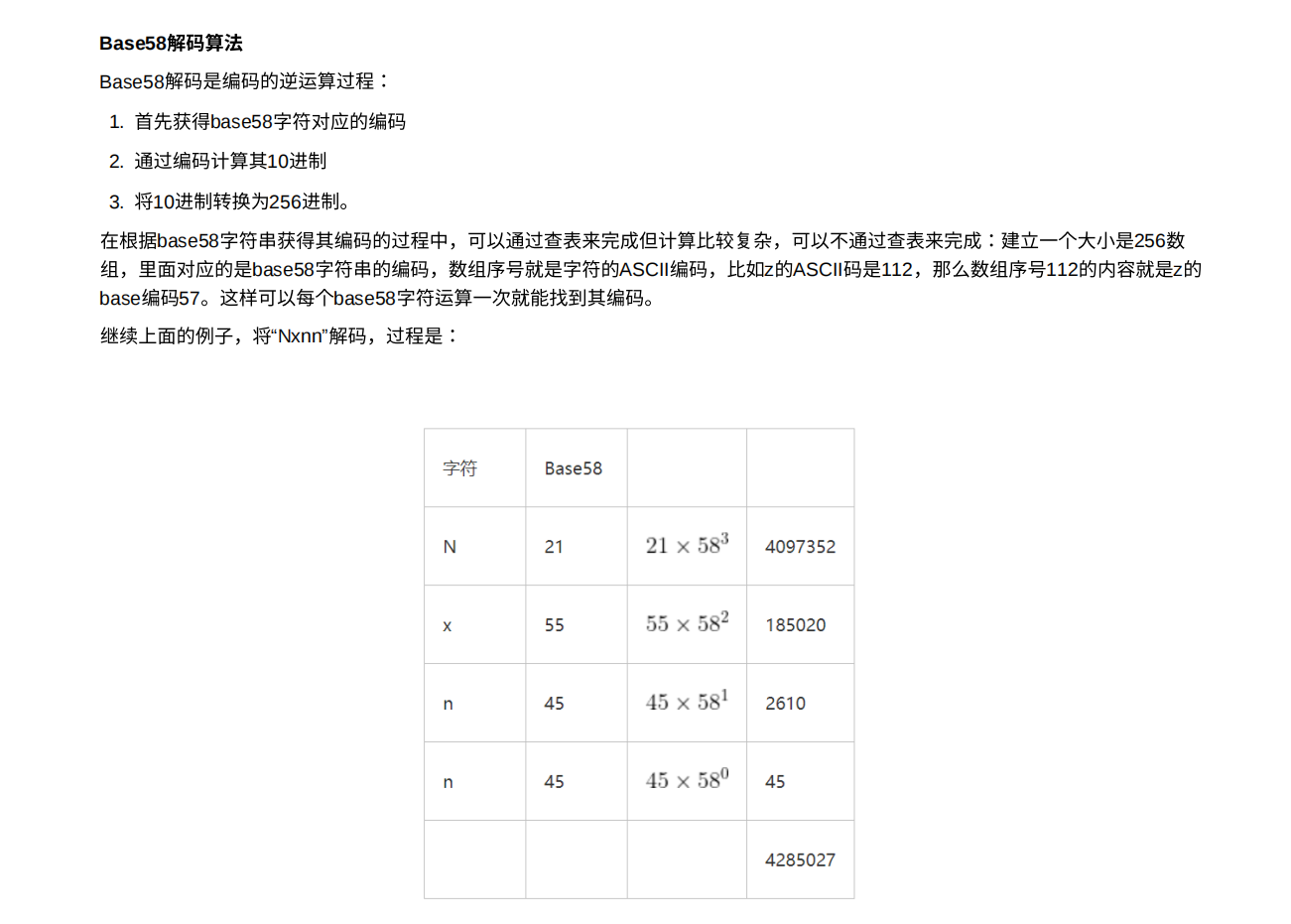
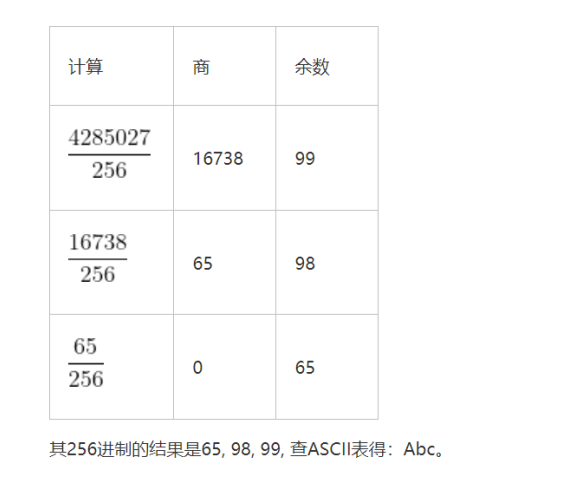
base58不需要key也能解出来

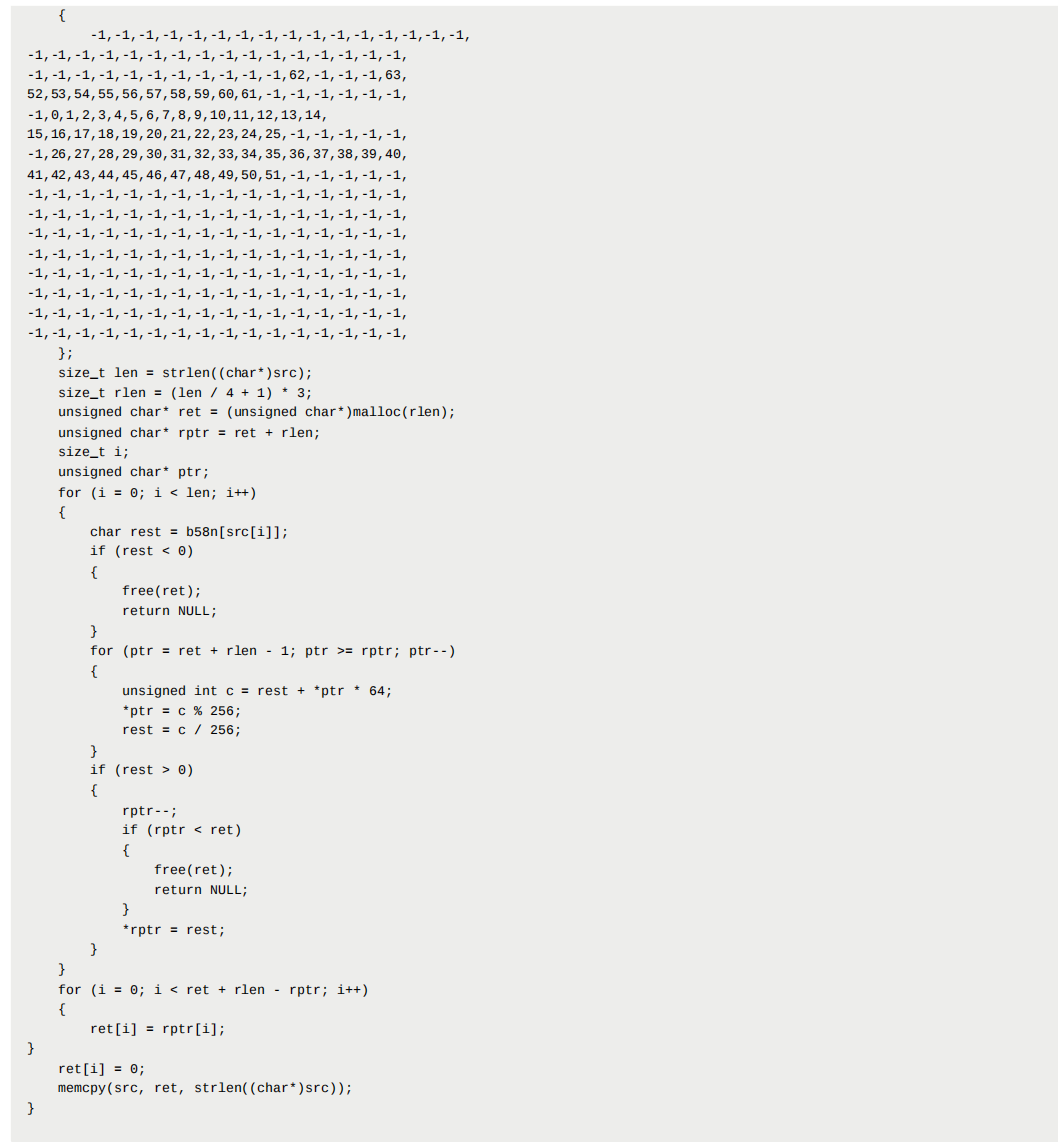
斐波那契数列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
v1 = fib_start;
v2 = &xmmword_408040;
xmmword_408040 = (__int128)_mm_load_si128((const __m128i *)&xmmword_405050);
v3 = dword_404010 + 4;
do
{
  v4 = v1;
  if ( v1 <= 0 )
  {
    v12 = 1;
  }
  else
  {
    v5 = 0;
    v6 = 0;
    v7 = 1;
    v8 = 1;
    v9 = 1;
    do
    {
      if ( (v4 & 1) != 0 )
      {
        v10 = v6;
        v6 = v7 * v8 + v5 * v6;
        v8 = v7 * v10 + v9 * v8;
      }
      v11 = v7 * v7;
      v7 *= v5 + v9;
      v5 = v11 + v5 * v5;
      v4 >>= 1;
      v9 = v9 * v9 + v11;
    }
    while ( v4 );
    v12 = v8;
  }
  ++v1;
  *(_DWORD *)v2 = v12;
  v2 = (__int128 *)((char *)v2 + 4);
}
while ( v1 != v3 );

IDEA

国际数据加密算法

IDEA是块加密，与DES一样，IDEA也处理64位明文块，但是其密钥有128位，IDEA也用扩展与混淆进行加密

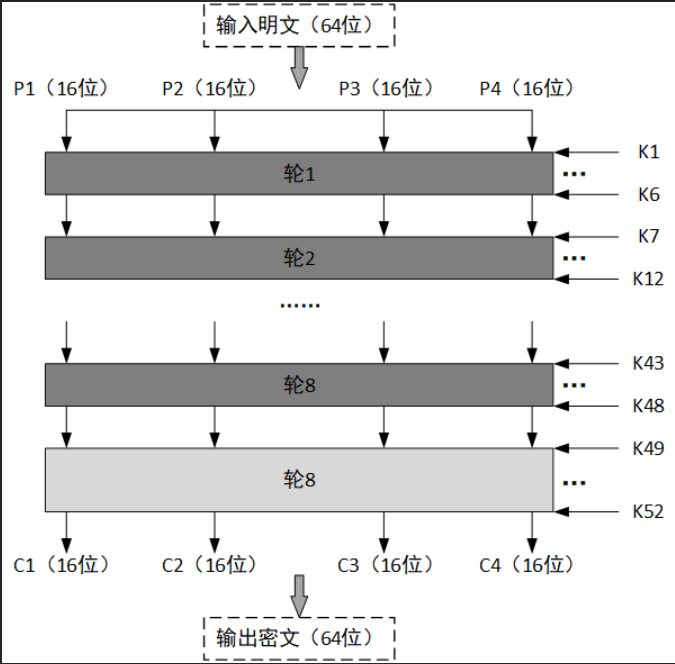
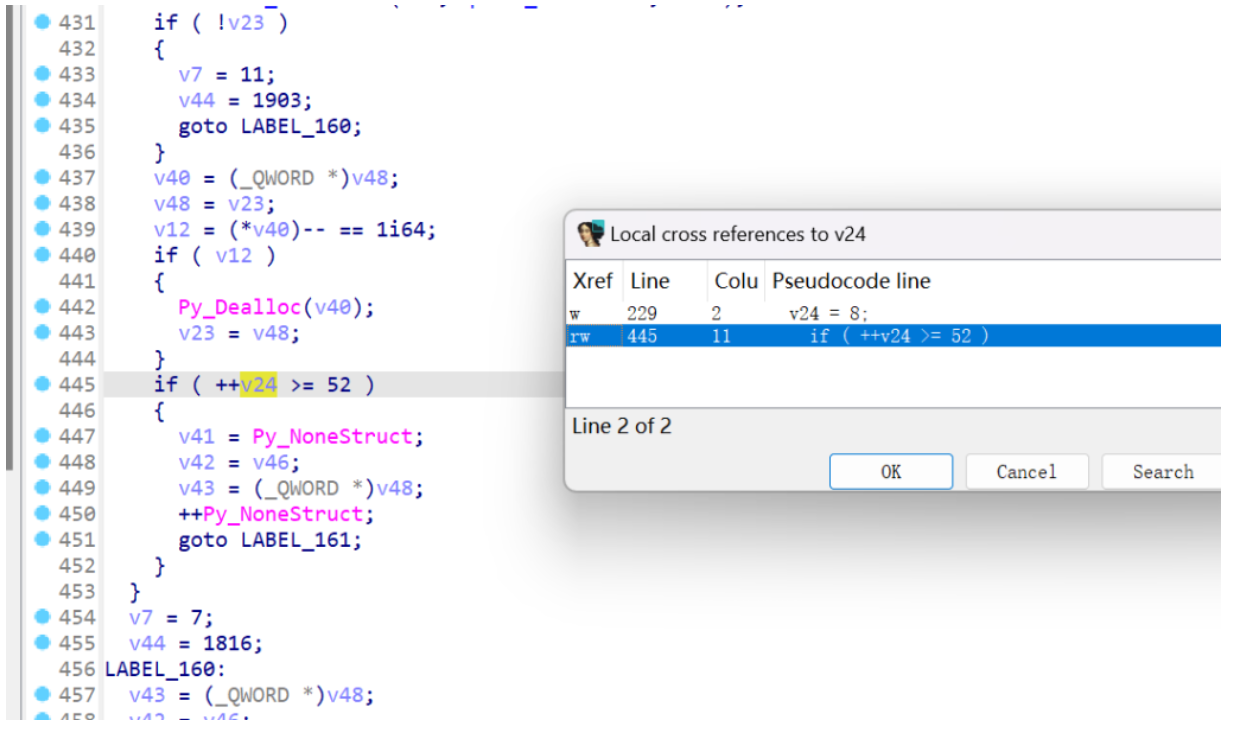
能看到0xffff，还有65537，还有加，异或的运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
#include <stdio.h>
#include <string.h>

typedef __uint32_t uint32_t;
typedef __int32_t int32_t;
typedef __uint16_t uint16_t;
typedef void (*idea_gen_key)(uint16_t[52], uint16_t[8]);

uint16_t mulMod65537(uint16_t a, uint16_t b) {
    uint32_t c;
    uint16_t hi, lo;

    if (a == 0)
        return -b + 1;
    if (b == 0)
        return -a + 1;

    c = (uint32_t)a * (uint32_t)b;
    hi = c >> 16;
    lo = c;

    if (lo > hi)
        return lo - hi;
    return lo - hi + 1;
}

int modInverse(int a, int m) {
    int m0 = m, t, q;
    int x0 = 0, x1 = 1;

    if (m == 1)
        return 0;

    while (a > 1) {
        // q is quotient
        q = a / m;
        t = m;

        // m is remainder now, process same as
        // Euclid's algo
        m = a % m;
        a = t;

        t = x0;
        x0 = x1 - q * x0;
        x1 = t;
    }

    // Make x1 positive
    if (x1 < 0)
        x1 += m0;

    return x1;
}

void encrypt(uint16_t subKey[52], uint16_t key[8]) {
    int i;

    // Generate encryption keys
    for (i = 0; i < 52; i++) {
        if (i < 8)
            subKey[i] = key[i];
        else if (i % 8 == 6)
            subKey[i] = (subKey[i - 7] << 9) | (subKey[i - 14] >> 7);
        else if (i % 8 == 7)
            subKey[i] = (subKey[i - 15] << 9) | (subKey[i - 14] >> 7);
        else
            subKey[i] = (subKey[i - 7] << 9) | (subKey[i - 6] >> 7);
    }
}

void decrypt(uint16_t subKey[52], uint16_t key[8]) {
    int i;
    uint16_t K[52];

    // Compute encryption keys
    encrypt(K, key);

    // Generate dencryption keys
    subKey[0] = modInverse(K[48], 65537);
    subKey[1] = -K[49];
    subKey[2] = -K[50];
    subKey[3] = modInverse(K[51], 65537);

    printf("Keys: %04X %04X %04X %04Xn", subKey[0], subKey[1], subKey[2],
         subKey[3]);

    for (i = 4; i < 52; i += 6) {
        subKey[i + 0] = K[52 - i - 2];
        subKey[i + 1] = K[52 - i - 1];

        subKey[i + 2] = modInverse(K[52 - i - 6], 65537);
        if (i == 46) {
            subKey[i + 3] = -K[52 - i - 5];
            subKey[i + 4] = -K[52 - i - 4];
        } else {
            subKey[i + 3] = -K[52 - i - 4];
            subKey[i + 4] = -K[52 - i - 5];
        }
        subKey[i + 5] = modInverse(K[52 - i - 3], 65537);

        printf("Keys: %04X %04X %04X %04X %04X %04Xn", subKey[i], subKey[i + 1],
           subKey[i + 2], subKey[i + 3], subKey[i + 4], subKey[i + 5]);
    }
}

void IDEA(uint16_t data[4], uint16_t key[8], idea_gen_key func) {
    int i;
    uint16_t subKey[52];

    // Generate keys
    func(subKey, key);

    uint16_t X0 = data[0];
    uint16_t X1 = data[1];
    uint16_t X2 = data[2];
    uint16_t X3 = data[3];
    uint16_t tmp1, tmp2;

    // Apply 8 rounds
    for (i = 0; i < 8; i++) {
        printf("%d:   %04X %04X %04X %04Xn", i, X0, X1, X2, X3);

        X0 = mulMod65537(X0, subKey[6 * i + 0]);  // Step 1
        X1 += subKey[6 * i + 1];                  // Step 2
        X2 += subKey[6 * i + 2];                  // Step 3
        X3 = mulMod65537(X3, subKey[6 * i + 3]);  // Step 4

        tmp1 = X0 ^ X2;  // Step 5
        tmp2 = X1 ^ X3;  // Step 6

        tmp1 = mulMod65537(tmp1, subKey[6 * i + 4]);  // Step 7
        tmp2 += tmp1;                                 // Step 8
        tmp2 = mulMod65537(tmp2, subKey[6 * i + 5]);  // Step 9
        tmp1 += tmp2;                                 // Step 10

        X0 ^= tmp2;
        X1 ^= tmp1;
        X2 ^= tmp2;
        X3 ^= tmp1;

        // Swap X1 and X2
        tmp1 = X1;
        X1 = X2;
        X2 = tmp1;
    }

    tmp1 = X1;
    tmp2 = X2;

    // Apply the half round
    data[0] = mulMod65537(X0, subKey[6 * i + 0]);
    data[1] = tmp2 + subKey[6 * i + 1];
    data[2] = tmp1 + subKey[6 * i + 2];
    data[3] = mulMod65537(X3, subKey[6 * i + 3]);
}

uint16_t binToInt(char* str) {
    int i;
    uint16_t size = strlen(str);
    uint16_t result = 0;
    uint16_t pow = 1;

    for (i = size - 1; i >= 0; i--) {
        if (str[i] == '1')
            result += pow;
        pow *= 2;
    }

    return result;
}

void convertStringToBin(char* str, uint16_t* data, uint16_t size) {
    int i, j = 0;
    int sizeBlock = sizeof(uint16_t) * 8;
    char block[sizeBlock + 1];

    for (i = 0; i < strlen(str) && i < size * sizeof(uint16_t);
       i += sizeof(uint16_t)) {
        strncpy(block, str, sizeBlock);
        block[sizeBlock] = '';

        data[j++] = binToInt(block);
        str += sizeBlock;
    }
}

int main() {
    char Data[] =
        "110111110100101101010100100010011000110001010001000000000000111011100000110011110000101001011001100001110000100010010110011011110011110010100010111100110011010000010110101101000111101011110111101001000110000010100001110101111100101000111010101110000100100011101100100101100110000011000111100010010000001001001001100000110111101111100011100011111111001001101111100010010100000101010111";
    char Key[128] = "01001110110010000111010101010110110101111011111010101001010010001011100010011110101000111100011111000010111100010011110000101110";

    uint16_t data[4*6];
    uint16_t key[8];

    convertStringToBin(Data, data, 4*6);
    convertStringToBin(Key, key, 8);
    for(int i=0;i<8;i++){
        printf("%x",key[i]);
    }

    // Print initial data
    printf("Initial data:   %04X %04X %04X %04Xn", data[0], data[1], data[2],
         data[3]);

    // Encrypt data
    // IDEA(data, key, encrypt);
    // printf("Encrypted data: %04X %04X %04X %04Xn", data[0], data[1], data[2],
    //      data[3]);

    // Decrypt data
    for(int i=0;i<6;i++) IDEA(data+4*i, key, decrypt);
    for(int i=0;i<24;i++) printf("%02x",data[i]);

    return 0;
}
知识点
Reverse常见算法
https://j1ya-22.github.io/2025/01/09/Reverse常见算法/
作者
j1ya
发布于
2025年1月9日
许可协议