浙江省省赛2025决赛wp

封榜前rank11最终圆梦省一，感谢队友带飞

Crypto

简单数学题

给了p和q和与差，直接相加相减得到p和q，后面直接解rsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
sum_pq = 15870713655456272818998868095126610389501417235762009793315127525027164306871912572802442396878309282140184445917718237547340279497682840149930939938364752
diff_pq = 836877201325346306269647062252443025692393860257609240213263622058769344319275021861627524327674665653956022396760961371531780934904914806513684926008590
e = 65537
c = 24161337439375469726924397660125738582989340535865292626109110404205047138648291988394300469831314677804449487707306159537988907383165388647811395995713768215918986950780552907040433887058197369446944754008620731946047814491450890197003594397567524722975778515304899628035385825818809556412246258855782770070
p=(sum_pq+diff_pq)//2
q=(sum_pq-diff_pq)//2
n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#b'DASCTF{ok_1+1_1s_ez_so_try2goldbachs}'

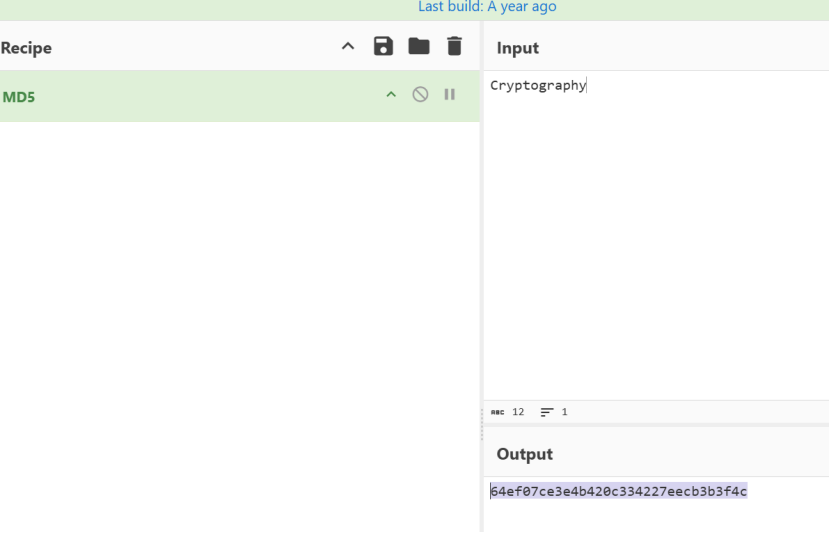
AES

cbc加密，给了key生成方法，密文和iv

md5生成key

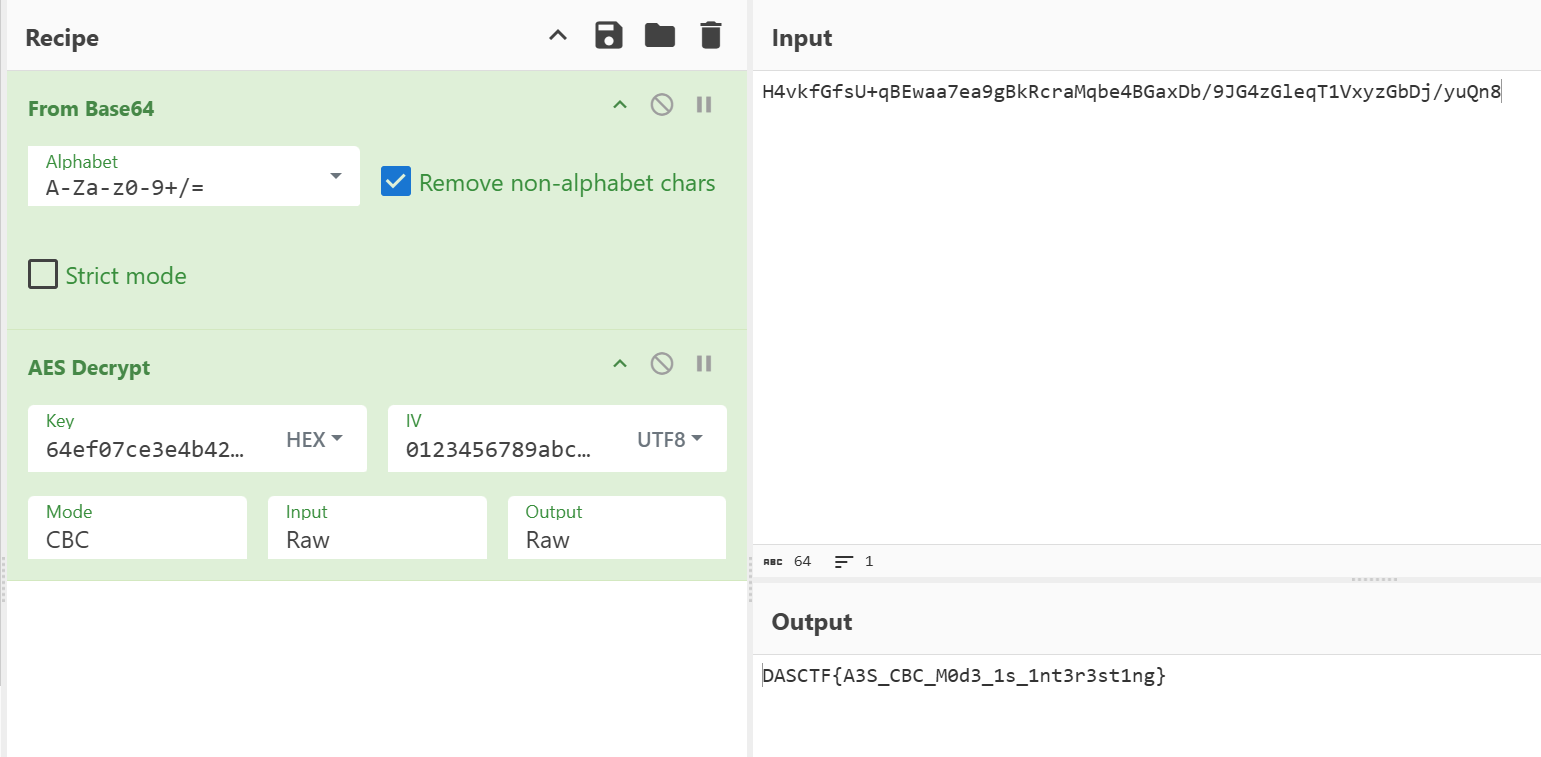
Base64

直接大厨解密

brainRSA-1

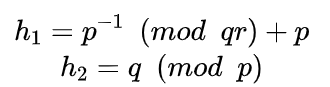
对于第一个hint可以这样变换

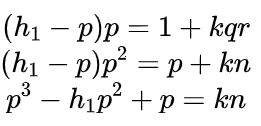
后面可以通过coppersmith解出p

如果m<p，那么mod n和mod p等价，所以后面phi可以用p-1来替代，这样假设能求出flag，但是求不出q无法验证

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *

n = 5896603616629976388681343986666930963006582028163928714145532756203237227730274711487003166019427105897965945120232260215410992579837484059292611073419586380525003988344574914431029827063806077732189986757809721088722985286036959879820708133146403409430195581622055470667222891220979774304289695570081825139756219411812254290165809196979501734849253222466549260913814647528326035080523330064602920600175311072318677328858357572118378221037611447468353988765857728693723209366913388728379914720462400719453373674212484217
e = 65537
c = 4221793406745090448159839492516441941495929321499567123472000442699162146372220161860225184236927618558037325910707307459975466187269605134233560519157016842737834824730633694720444565009425747524144994992594172304437752960220406217437575205487944977177237131899857115110278358933279454006801350405232784421011170963118967018535823980784090051685902395650907846245302374549113152846903151411198578675291462184512223571295652757739539096560166939391938607962013244587459259461981764347874215325536867806205636381420076263
h1 = 86682368885754481246073975629273374009118678612781484142142233010648189936701991035424570227832428961089155099087480306450429844896945882196738935354601757929219259054136973233403527177389212490240890908590489235856630191642125591379880282065718229563065862910111151238228617993062409710807546317753676418582796716091984804706084632849079312032895792218093262044435
h2 = 507302396516541130096005191243501282527086130677192353031178107965055262527263846570902262566241833462389458229472609073835612242905629592637875830766904


PR.<x> = PolynomialRing(Zmod(n))
f = x^3 - h1*x^2+x
p = int(f.small_roots(X=2^512,beta=0.4,epsilon=0.01)[1])
print(p)

d = inverse(e,p-1)
m = pow(c,d,p)
print(long_to_bytes(m))
# b'flag{V#@Ry_@ASSy_Pr013L@m-for_RsA!}'

Reverse

你是我的天命人吗

第一个函数是VirtualProtect自解密

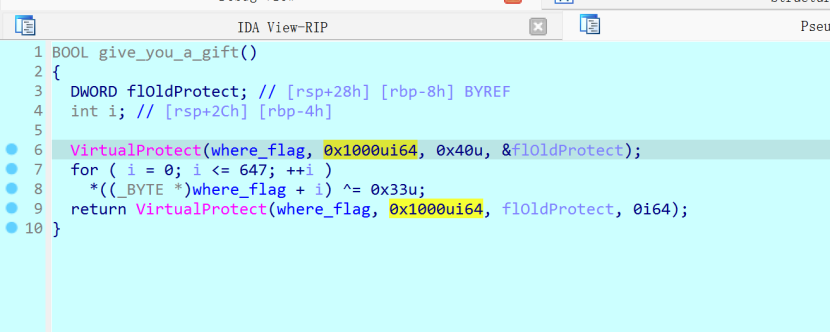
第二个函数进入之后创建函数

输入先异或i再转成hex

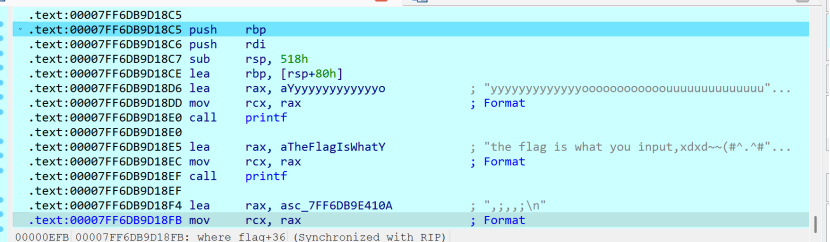
直接逆向

1
2
3
4
5
s='4440514050437D3E386C3A3F3E6F386D232124202D7420742C2F2E282525782D124344471015405A'
print(len(s))
for i in range(0,len(s),2):
    print(chr(int(s[i:i+2],16)^(i//2)),end="")
#DASCTF{90e042b6b30639a6c464398f22bfd40f}

androidtest

jadx反编译不完全，用jeb打开发现base32的表

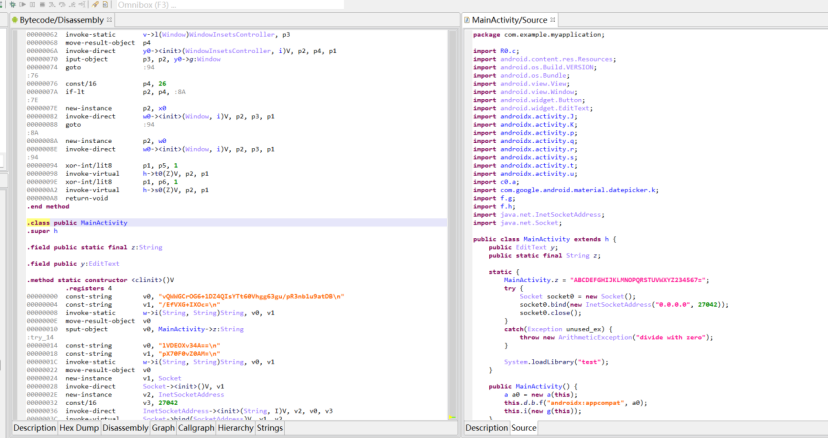
so层下存在密文

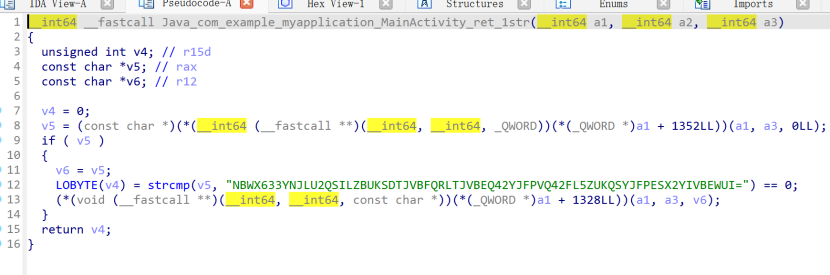
先base32解密

比赛期间通过测试之后猜测再xor44能得到flag

1
2
3
4
a=[0x68 ,0x6d ,0x7f ,0x6f ,0x78 ,0x6a ,0x57 ,0x4d ,0x42 ,0x48 ,0x5e ,0x43 ,0x45 ,0x48 ,0x73 ,0x4d ,0x42 ,0x58 ,0x45 ,0x73 ,0x4d ,0x42 ,0x48 ,0x73 ,0x58 ,0x49 ,0x5f ,0x58 ,0x73 ,0x45 ,0x5f ,0x73 ,0x45 ,0x42 ,0x58 ,0x49 ,0x5e ,0x49 ,0x5f ,0x58 ,0x45 ,0x42 ,0x4b ,0x51]
for i in range(len(a)):
    print(chr(a[i]^44),end="")
#DASCTF{android_anti_and_test_is_interesting}

交叉引用ret_str方法找到关键加密，Onclick里面先执行xor 44再base32加密后和密文比较

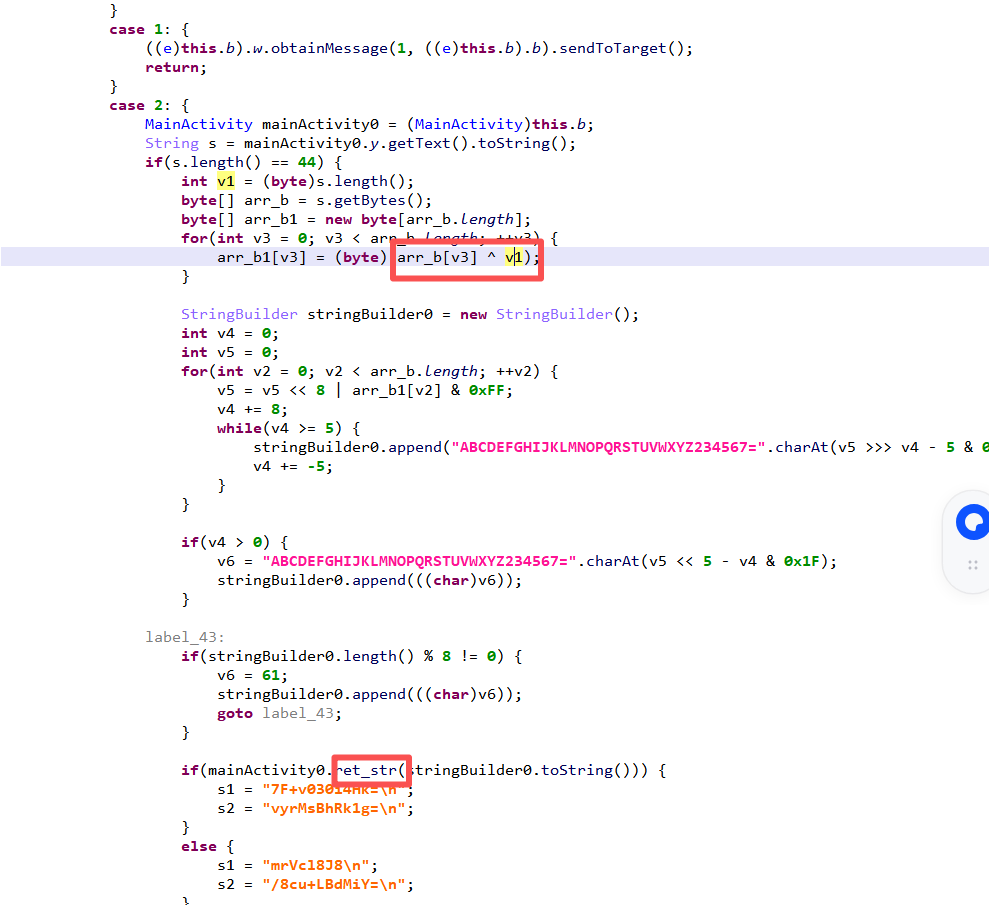
Warning-1

输入作为参数传入

调试的时候参数放到parameters里

trace xor

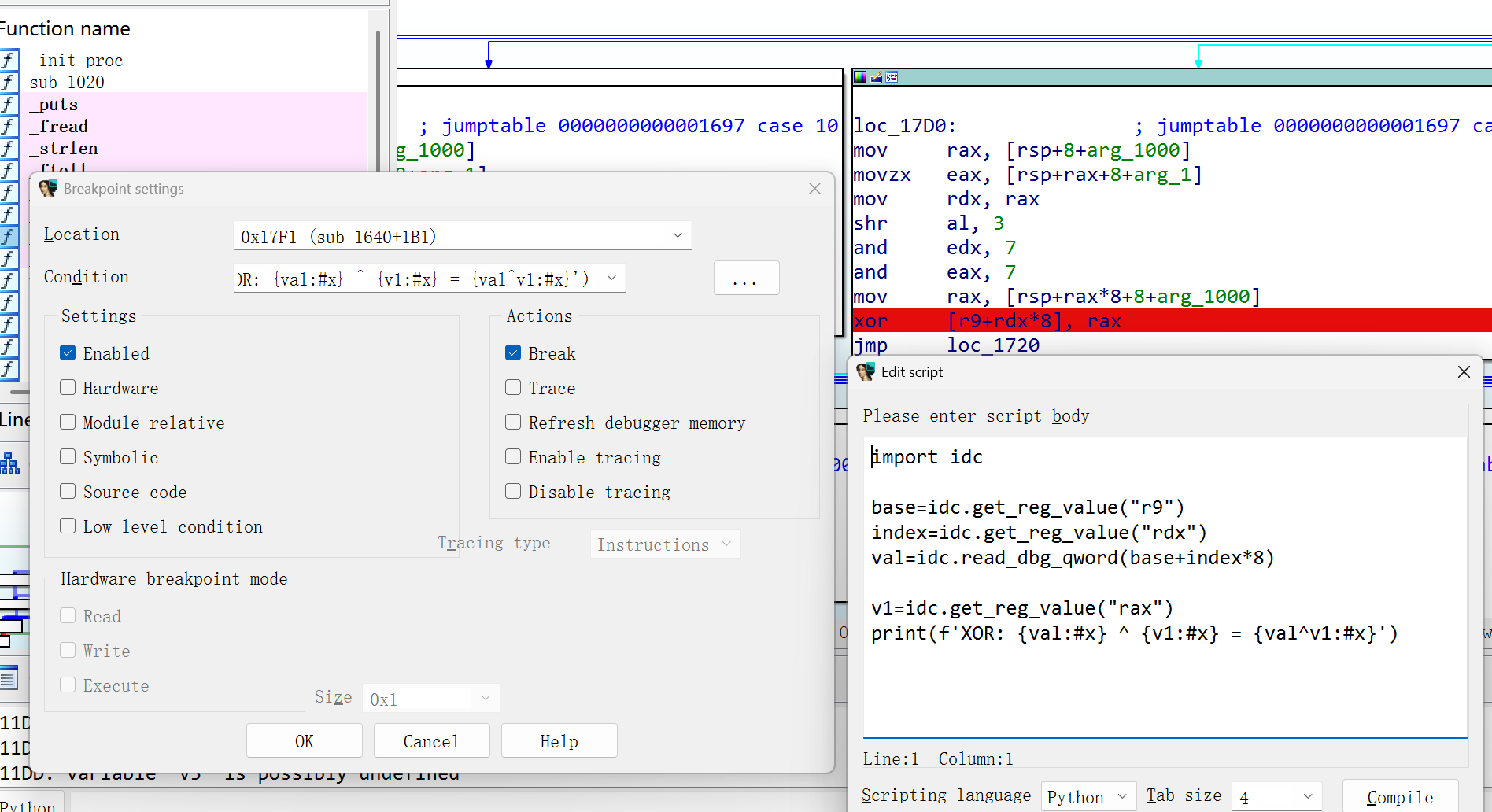
trace cmp

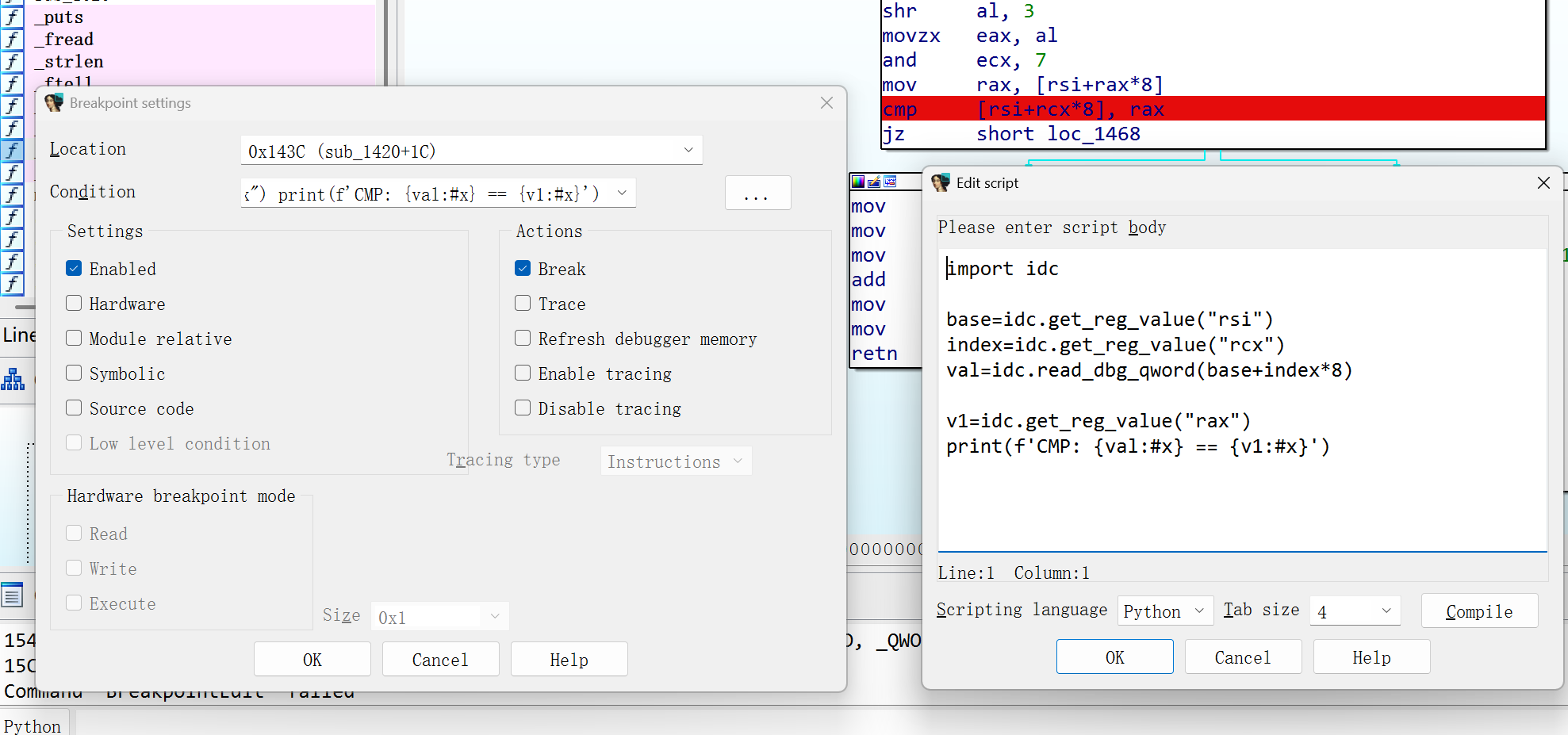
上述trace后得到如下内容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
XOR: 0x31 ^ 0x0 = 0x31
CMP: 0x2e == 0x1
XOR: 0x31 ^ 0x1 = 0x30
CMP: 0x2e == 0x2
XOR: 0x31 ^ 0x2 = 0x33
CMP: 0x2e == 0x3
XOR: 0x31 ^ 0x3 = 0x32
CMP: 0x2e == 0x4
XOR: 0x31 ^ 0x4 = 0x35
CMP: 0x2e == 0x5
XOR: 0x31 ^ 0x5 = 0x34
CMP: 0x2e == 0x6
XOR: 0x31 ^ 0x6 = 0x37
CMP: 0x2e == 0x7
XOR: 0x31 ^ 0x7 = 0x36
CMP: 0x2e == 0x8
XOR: 0x31 ^ 0x8 = 0x39
CMP: 0x2e == 0x9
XOR: 0x31 ^ 0x9 = 0x38
CMP: 0x2e == 0xa
XOR: 0x31 ^ 0xa = 0x3b
CMP: 0x2e == 0xb
XOR: 0x31 ^ 0xb = 0x3a
CMP: 0x2e == 0xc
XOR: 0x31 ^ 0xc = 0x3d
CMP: 0x2e == 0xd
XOR: 0x31 ^ 0xd = 0x3c
CMP: 0x2e == 0xe
XOR: 0x31 ^ 0xe = 0x3f
CMP: 0x2e == 0xf
XOR: 0x31 ^ 0xf = 0x3e
CMP: 0x2e == 0x10
XOR: 0x31 ^ 0x10 = 0x21
CMP: 0x2e == 0x11
XOR: 0x31 ^ 0x11 = 0x20
CMP: 0x2e == 0x12
XOR: 0x31 ^ 0x12 = 0x23
CMP: 0x2e == 0x13
XOR: 0x31 ^ 0x13 = 0x22
CMP: 0x2e == 0x14
XOR: 0x31 ^ 0x14 = 0x25
CMP: 0x2e == 0x15
XOR: 0x31 ^ 0x15 = 0x24
CMP: 0x2e == 0x16
XOR: 0x31 ^ 0x16 = 0x27
CMP: 0x2e == 0x17
XOR: 0x31 ^ 0x17 = 0x26
CMP: 0x2e == 0x18
XOR: 0x31 ^ 0x18 = 0x29
CMP: 0x2e == 0x19
XOR: 0x31 ^ 0x19 = 0x28
CMP: 0x2e == 0x1a
XOR: 0x31 ^ 0x1a = 0x2b
CMP: 0x2e == 0x1b
XOR: 0x31 ^ 0x1b = 0x2a
CMP: 0x2e == 0x1c
XOR: 0x31 ^ 0x1c = 0x2d
CMP: 0x2e == 0x1d
XOR: 0x31 ^ 0x1d = 0x2c
CMP: 0x2e == 0x1e
XOR: 0x31 ^ 0x1e = 0x2f
CMP: 0x2e == 0x1f
XOR: 0x31 ^ 0x1f = 0x2e
CMP: 0x2e == 0x20
XOR: 0x31 ^ 0x20 = 0x11
CMP: 0x2e == 0x21
XOR: 0x31 ^ 0x21 = 0x10
CMP: 0x2e == 0x22
XOR: 0x31 ^ 0x22 = 0x13
CMP: 0x2e == 0x23
XOR: 0x31 ^ 0x23 = 0x12
CMP: 0x2e == 0x24
XOR: 0x31 ^ 0x24 = 0x15
CMP: 0x2e == 0x25
XOR: 0x31 ^ 0x25 = 0x14
CMP: 0x2e == 0x26
XOR: 0x31 ^ 0x26 = 0x17
CMP: 0x2e == 0x27
XOR: 0x31 ^ 0x27 = 0x16
CMP: 0x2e == 0x28
XOR: 0x31 ^ 0x28 = 0x19
CMP: 0x2e == 0x29
XOR: 0x31 ^ 0x29 = 0x18
CMP: 0x2e == 0x2a
XOR: 0x31 ^ 0x2a = 0x1b
CMP: 0x2e == 0x2b
XOR: 0x31 ^ 0x2b = 0x1a
CMP: 0x2e == 0x2c
XOR: 0x31 ^ 0x2c = 0x1d
CMP: 0x2e == 0x2d
XOR: 0x31 ^ 0x2d = 0x1c
CMP: 0x2e == 0x2e
CMP: 0x100 == 0x1
CMP: 0x100 == 0x2
CMP: 0x100 == 0x3
CMP: 0x100 == 0x4
CMP: 0x100 == 0x5
CMP: 0x100 == 0x6
CMP: 0x100 == 0x7
CMP: 0x100 == 0x8
CMP: 0x100 == 0x9
CMP: 0x100 == 0xa
CMP: 0x100 == 0xb
CMP: 0x100 == 0xc
CMP: 0x100 == 0xd
CMP: 0x100 == 0xe
CMP: 0x100 == 0xf
CMP: 0x100 == 0x10
CMP: 0x100 == 0x11
CMP: 0x100 == 0x12
CMP: 0x100 == 0x13
CMP: 0x100 == 0x14
CMP: 0x100 == 0x15
CMP: 0x100 == 0x16
CMP: 0x100 == 0x17
CMP: 0x100 == 0x18
CMP: 0x100 == 0x19
CMP: 0x100 == 0x1a
CMP: 0x100 == 0x1b
CMP: 0x100 == 0x1c
CMP: 0x100 == 0x1d
CMP: 0x100 == 0x1e
CMP: 0x100 == 0x1f
CMP: 0x100 == 0x20
CMP: 0x100 == 0x21
CMP: 0x100 == 0x22
CMP: 0x100 == 0x23
CMP: 0x100 == 0x24
CMP: 0x100 == 0x25
CMP: 0x100 == 0x26
CMP: 0x100 == 0x27
CMP: 0x100 == 0x28
CMP: 0x100 == 0x29
CMP: 0x100 == 0x2a
CMP: 0x100 == 0x2b
CMP: 0x100 == 0x2c
CMP: 0x100 == 0x2d
CMP: 0x100 == 0x2e
CMP: 0x100 == 0x2f
CMP: 0x100 == 0x30
CMP: 0x100 == 0x31
CMP: 0x100 == 0x32
CMP: 0x100 == 0x33
CMP: 0x100 == 0x34
CMP: 0x100 == 0x35
CMP: 0x100 == 0x36
CMP: 0x100 == 0x37
CMP: 0x100 == 0x38
CMP: 0x100 == 0x39
CMP: 0x100 == 0x3a
CMP: 0x100 == 0x3b
CMP: 0x100 == 0x3c
CMP: 0x100 == 0x3d
CMP: 0x100 == 0x3e
CMP: 0x100 == 0x3f
CMP: 0x100 == 0x40
CMP: 0x100 == 0x41
CMP: 0x100 == 0x42
CMP: 0x100 == 0x43
CMP: 0x100 == 0x44
CMP: 0x100 == 0x45
CMP: 0x100 == 0x46
CMP: 0x100 == 0x47
CMP: 0x100 == 0x48
CMP: 0x100 == 0x49
CMP: 0x100 == 0x4a
CMP: 0x100 == 0x4b
CMP: 0x100 == 0x4c
CMP: 0x100 == 0x4d
CMP: 0x100 == 0x4e
CMP: 0x100 == 0x4f
CMP: 0x100 == 0x50
CMP: 0x100 == 0x51
CMP: 0x100 == 0x52
CMP: 0x100 == 0x53
CMP: 0x100 == 0x54
CMP: 0x100 == 0x55
CMP: 0x100 == 0x56
CMP: 0x100 == 0x57
CMP: 0x100 == 0x58
CMP: 0x100 == 0x59
CMP: 0x100 == 0x5a
CMP: 0x100 == 0x5b
CMP: 0x100 == 0x5c
CMP: 0x100 == 0x5d
CMP: 0x100 == 0x5e
CMP: 0x100 == 0x5f
CMP: 0x100 == 0x60
CMP: 0x100 == 0x61
CMP: 0x100 == 0x62
CMP: 0x100 == 0x63
CMP: 0x100 == 0x64
CMP: 0x100 == 0x65
CMP: 0x100 == 0x66
CMP: 0x100 == 0x67
CMP: 0x100 == 0x68
CMP: 0x100 == 0x69
CMP: 0x100 == 0x6a
CMP: 0x100 == 0x6b
CMP: 0x100 == 0x6c
CMP: 0x100 == 0x6d
CMP: 0x100 == 0x6e
CMP: 0x100 == 0x6f
CMP: 0x100 == 0x70
CMP: 0x100 == 0x71
CMP: 0x100 == 0x72
CMP: 0x100 == 0x73
CMP: 0x100 == 0x74
CMP: 0x100 == 0x75
CMP: 0x100 == 0x76
CMP: 0x100 == 0x77
CMP: 0x100 == 0x78
CMP: 0x100 == 0x79
CMP: 0x100 == 0x7a
CMP: 0x100 == 0x7b
CMP: 0x100 == 0x7c
CMP: 0x100 == 0x7d
CMP: 0x100 == 0x7e
CMP: 0x100 == 0x7f
CMP: 0x100 == 0x80
CMP: 0x100 == 0x81
CMP: 0x100 == 0x82
CMP: 0x100 == 0x83
CMP: 0x100 == 0x84
CMP: 0x100 == 0x85
CMP: 0x100 == 0x86
CMP: 0x100 == 0x87
CMP: 0x100 == 0x88
CMP: 0x100 == 0x89
CMP: 0x100 == 0x8a
CMP: 0x100 == 0x8b
CMP: 0x100 == 0x8c
CMP: 0x100 == 0x8d
CMP: 0x100 == 0x8e
CMP: 0x100 == 0x8f
CMP: 0x100 == 0x90
CMP: 0x100 == 0x91
CMP: 0x100 == 0x92
CMP: 0x100 == 0x93
CMP: 0x100 == 0x94
CMP: 0x100 == 0x95
CMP: 0x100 == 0x96
CMP: 0x100 == 0x97
CMP: 0x100 == 0x98
CMP: 0x100 == 0x99
CMP: 0x100 == 0x9a
CMP: 0x100 == 0x9b
CMP: 0x100 == 0x9c
CMP: 0x100 == 0x9d
CMP: 0x100 == 0x9e
CMP: 0x100 == 0x9f
CMP: 0x100 == 0xa0
CMP: 0x100 == 0xa1
CMP: 0x100 == 0xa2
CMP: 0x100 == 0xa3
CMP: 0x100 == 0xa4
CMP: 0x100 == 0xa5
CMP: 0x100 == 0xa6
CMP: 0x100 == 0xa7
CMP: 0x100 == 0xa8
CMP: 0x100 == 0xa9
CMP: 0x100 == 0xaa
CMP: 0x100 == 0xab
CMP: 0x100 == 0xac
CMP: 0x100 == 0xad
CMP: 0x100 == 0xae
CMP: 0x100 == 0xaf
CMP: 0x100 == 0xb0
CMP: 0x100 == 0xb1
CMP: 0x100 == 0xb2
CMP: 0x100 == 0xb3
CMP: 0x100 == 0xb4
CMP: 0x100 == 0xb5
CMP: 0x100 == 0xb6
CMP: 0x100 == 0xb7
CMP: 0x100 == 0xb8
CMP: 0x100 == 0xb9
CMP: 0x100 == 0xba
CMP: 0x100 == 0xbb
CMP: 0x100 == 0xbc
CMP: 0x100 == 0xbd
CMP: 0x100 == 0xbe
CMP: 0x100 == 0xbf
CMP: 0x100 == 0xc0
CMP: 0x100 == 0xc1
CMP: 0x100 == 0xc2
CMP: 0x100 == 0xc3
CMP: 0x100 == 0xc4
CMP: 0x100 == 0xc5
CMP: 0x100 == 0xc6
CMP: 0x100 == 0xc7
CMP: 0x100 == 0xc8
CMP: 0x100 == 0xc9
CMP: 0x100 == 0xca
CMP: 0x100 == 0xcb
CMP: 0x100 == 0xcc
CMP: 0x100 == 0xcd
CMP: 0x100 == 0xce
CMP: 0x100 == 0xcf
CMP: 0x100 == 0xd0
CMP: 0x100 == 0xd1
CMP: 0x100 == 0xd2
CMP: 0x100 == 0xd3
CMP: 0x100 == 0xd4
CMP: 0x100 == 0xd5
CMP: 0x100 == 0xd6
CMP: 0x100 == 0xd7
CMP: 0x100 == 0xd8
CMP: 0x100 == 0xd9
CMP: 0x100 == 0xda
CMP: 0x100 == 0xdb
CMP: 0x100 == 0xdc
CMP: 0x100 == 0xdd
CMP: 0x100 == 0xde
CMP: 0x100 == 0xdf
CMP: 0x100 == 0xe0
CMP: 0x100 == 0xe1
CMP: 0x100 == 0xe2
CMP: 0x100 == 0xe3
CMP: 0x100 == 0xe4
CMP: 0x100 == 0xe5
CMP: 0x100 == 0xe6
CMP: 0x100 == 0xe7
CMP: 0x100 == 0xe8
CMP: 0x100 == 0xe9
CMP: 0x100 == 0xea
CMP: 0x100 == 0xeb
CMP: 0x100 == 0xec
CMP: 0x100 == 0xed
CMP: 0x100 == 0xee
CMP: 0x100 == 0xef
CMP: 0x100 == 0xf0
CMP: 0x100 == 0xf1
CMP: 0x100 == 0xf2
CMP: 0x100 == 0xf3
CMP: 0x100 == 0xf4
CMP: 0x100 == 0xf5
CMP: 0x100 == 0xf6
CMP: 0x100 == 0xf7
CMP: 0x100 == 0xf8
CMP: 0x100 == 0xf9
CMP: 0x100 == 0xfa
CMP: 0x100 == 0xfb
CMP: 0x100 == 0xfc
CMP: 0x100 == 0xfd
CMP: 0x100 == 0xfe
CMP: 0x100 == 0xff
CMP: 0x100 == 0x100
CMP: 0x100 == 0x1
CMP: 0x100 == 0x2
CMP: 0x100 == 0x3
CMP: 0x100 == 0x4
CMP: 0x100 == 0x5
CMP: 0x100 == 0x6
CMP: 0x100 == 0x7
CMP: 0x100 == 0x8
CMP: 0x100 == 0x9
CMP: 0x100 == 0xa
CMP: 0x100 == 0xb
CMP: 0x100 == 0xc
CMP: 0x100 == 0xd
CMP: 0x100 == 0xe
CMP: 0x100 == 0xf
CMP: 0x100 == 0x10
CMP: 0x100 == 0x11
CMP: 0x100 == 0x12
CMP: 0x100 == 0x13
CMP: 0x100 == 0x14
CMP: 0x100 == 0x15
CMP: 0x100 == 0x16
CMP: 0x100 == 0x17
CMP: 0x100 == 0x18
CMP: 0x100 == 0x19
CMP: 0x100 == 0x1a
CMP: 0x100 == 0x1b
CMP: 0x100 == 0x1c
CMP: 0x100 == 0x1d
CMP: 0x100 == 0x1e
CMP: 0x100 == 0x1f
CMP: 0x100 == 0x20
CMP: 0x100 == 0x21
CMP: 0x100 == 0x22
CMP: 0x100 == 0x23
CMP: 0x100 == 0x24
CMP: 0x100 == 0x25
CMP: 0x100 == 0x26
CMP: 0x100 == 0x27
CMP: 0x100 == 0x28
CMP: 0x100 == 0x29
CMP: 0x100 == 0x2a
CMP: 0x100 == 0x2b
CMP: 0x100 == 0x2c
CMP: 0x100 == 0x2d
CMP: 0x100 == 0x2e
CMP: 0x100 == 0x2f
CMP: 0x100 == 0x30
CMP: 0x100 == 0x31
CMP: 0x100 == 0x32
CMP: 0x100 == 0x33
CMP: 0x100 == 0x34
CMP: 0x100 == 0x35
CMP: 0x100 == 0x36
CMP: 0x100 == 0x37
CMP: 0x100 == 0x38
CMP: 0x100 == 0x39
CMP: 0x100 == 0x3a
CMP: 0x100 == 0x3b
CMP: 0x100 == 0x3c
CMP: 0x100 == 0x3d
CMP: 0x100 == 0x3e
CMP: 0x100 == 0x3f
CMP: 0x100 == 0x40
CMP: 0x100 == 0x41
CMP: 0x100 == 0x42
CMP: 0x100 == 0x43
CMP: 0x100 == 0x44
CMP: 0x100 == 0x45
CMP: 0x100 == 0x46
CMP: 0x100 == 0x47
CMP: 0x100 == 0x48
CMP: 0x100 == 0x49
CMP: 0x100 == 0x4a
CMP: 0x100 == 0x4b
CMP: 0x100 == 0x4c
CMP: 0x100 == 0x4d
CMP: 0x100 == 0x4e
CMP: 0x100 == 0x4f
CMP: 0x100 == 0x50
CMP: 0x100 == 0x51
CMP: 0x100 == 0x52
CMP: 0x100 == 0x53
CMP: 0x100 == 0x54
CMP: 0x100 == 0x55
CMP: 0x100 == 0x56
CMP: 0x100 == 0x57
CMP: 0x100 == 0x58
CMP: 0x100 == 0x59
CMP: 0x100 == 0x5a
CMP: 0x100 == 0x5b
CMP: 0x100 == 0x5c
CMP: 0x100 == 0x5d
CMP: 0x100 == 0x5e
CMP: 0x100 == 0x5f
CMP: 0x100 == 0x60
CMP: 0x100 == 0x61
CMP: 0x100 == 0x62
CMP: 0x100 == 0x63
CMP: 0x100 == 0x64
CMP: 0x100 == 0x65
CMP: 0x100 == 0x66
CMP: 0x100 == 0x67
CMP: 0x100 == 0x68
CMP: 0x100 == 0x69
CMP: 0x100 == 0x6a
CMP: 0x100 == 0x6b
CMP: 0x100 == 0x6c
CMP: 0x100 == 0x6d
CMP: 0x100 == 0x6e
CMP: 0x100 == 0x6f
CMP: 0x100 == 0x70
CMP: 0x100 == 0x71
CMP: 0x100 == 0x72
CMP: 0x100 == 0x73
CMP: 0x100 == 0x74
CMP: 0x100 == 0x75
CMP: 0x100 == 0x76
CMP: 0x100 == 0x77
CMP: 0x100 == 0x78
CMP: 0x100 == 0x79
CMP: 0x100 == 0x7a
CMP: 0x100 == 0x7b
CMP: 0x100 == 0x7c
CMP: 0x100 == 0x7d
CMP: 0x100 == 0x7e
CMP: 0x100 == 0x7f
CMP: 0x100 == 0x80
CMP: 0x100 == 0x81
CMP: 0x100 == 0x82
CMP: 0x100 == 0x83
CMP: 0x100 == 0x84
CMP: 0x100 == 0x85
CMP: 0x100 == 0x86
CMP: 0x100 == 0x87
CMP: 0x100 == 0x88
CMP: 0x100 == 0x89
CMP: 0x100 == 0x8a
CMP: 0x100 == 0x8b
CMP: 0x100 == 0x8c
CMP: 0x100 == 0x8d
CMP: 0x100 == 0x8e
CMP: 0x100 == 0x8f
CMP: 0x100 == 0x90
CMP: 0x100 == 0x91
CMP: 0x100 == 0x92
CMP: 0x100 == 0x93
CMP: 0x100 == 0x94
CMP: 0x100 == 0x95
CMP: 0x100 == 0x96
CMP: 0x100 == 0x97
CMP: 0x100 == 0x98
CMP: 0x100 == 0x99
CMP: 0x100 == 0x9a
CMP: 0x100 == 0x9b
CMP: 0x100 == 0x9c
CMP: 0x100 == 0x9d
CMP: 0x100 == 0x9e
CMP: 0x100 == 0x9f
CMP: 0x100 == 0xa0
CMP: 0x100 == 0xa1
CMP: 0x100 == 0xa2
CMP: 0x100 == 0xa3
CMP: 0x100 == 0xa4
CMP: 0x100 == 0xa5
CMP: 0x100 == 0xa6
CMP: 0x100 == 0xa7
CMP: 0x100 == 0xa8
CMP: 0x100 == 0xa9
CMP: 0x100 == 0xaa
CMP: 0x100 == 0xab
CMP: 0x100 == 0xac
CMP: 0x100 == 0xad
CMP: 0x100 == 0xae
CMP: 0x100 == 0xaf
CMP: 0x100 == 0xb0
CMP: 0x100 == 0xb1
CMP: 0x100 == 0xb2
CMP: 0x100 == 0xb3
CMP: 0x100 == 0xb4
CMP: 0x100 == 0xb5
CMP: 0x100 == 0xb6
CMP: 0x100 == 0xb7
CMP: 0x100 == 0xb8
CMP: 0x100 == 0xb9
CMP: 0x100 == 0xba
CMP: 0x100 == 0xbb
CMP: 0x100 == 0xbc
CMP: 0x100 == 0xbd
CMP: 0x100 == 0xbe
CMP: 0x100 == 0xbf
CMP: 0x100 == 0xc0
CMP: 0x100 == 0xc1
CMP: 0x100 == 0xc2
CMP: 0x100 == 0xc3
CMP: 0x100 == 0xc4
CMP: 0x100 == 0xc5
CMP: 0x100 == 0xc6
CMP: 0x100 == 0xc7
CMP: 0x100 == 0xc8
CMP: 0x100 == 0xc9
CMP: 0x100 == 0xca
CMP: 0x100 == 0xcb
CMP: 0x100 == 0xcc
CMP: 0x100 == 0xcd
CMP: 0x100 == 0xce
CMP: 0x100 == 0xcf
CMP: 0x100 == 0xd0
CMP: 0x100 == 0xd1
CMP: 0x100 == 0xd2
CMP: 0x100 == 0xd3
CMP: 0x100 == 0xd4
CMP: 0x100 == 0xd5
CMP: 0x100 == 0xd6
CMP: 0x100 == 0xd7
CMP: 0x100 == 0xd8
CMP: 0x100 == 0xd9
CMP: 0x100 == 0xda
CMP: 0x100 == 0xdb
CMP: 0x100 == 0xdc
CMP: 0x100 == 0xdd
CMP: 0x100 == 0xde
CMP: 0x100 == 0xdf
CMP: 0x100 == 0xe0
CMP: 0x100 == 0xe1
CMP: 0x100 == 0xe2
CMP: 0x100 == 0xe3
CMP: 0x100 == 0xe4
CMP: 0x100 == 0xe5
CMP: 0x100 == 0xe6
CMP: 0x100 == 0xe7
CMP: 0x100 == 0xe8
CMP: 0x100 == 0xe9
CMP: 0x100 == 0xea
CMP: 0x100 == 0xeb
CMP: 0x100 == 0xec
CMP: 0x100 == 0xed
CMP: 0x100 == 0xee
CMP: 0x100 == 0xef
CMP: 0x100 == 0xf0
CMP: 0x100 == 0xf1
CMP: 0x100 == 0xf2
CMP: 0x100 == 0xf3
CMP: 0x100 == 0xf4
CMP: 0x100 == 0xf5
CMP: 0x100 == 0xf6
CMP: 0x100 == 0xf7
CMP: 0x100 == 0xf8
CMP: 0x100 == 0xf9
CMP: 0x100 == 0xfa
CMP: 0x100 == 0xfb
CMP: 0x100 == 0xfc
CMP: 0x100 == 0xfd
CMP: 0x100 == 0xfe
CMP: 0x100 == 0xff
CMP: 0x100 == 0x100
XOR: 0x31 ^ 0x50 = 0x61
CMP: 0x1 == 0x2e
XOR: 0x30 ^ 0x67 = 0x57
CMP: 0x2 == 0x2e
XOR: 0x33 ^ 0x21 = 0x12
CMP: 0x3 == 0x2e
XOR: 0x32 ^ 0x2b = 0x19
CMP: 0x4 == 0x2e
XOR: 0x35 ^ 0xce = 0xfb
CMP: 0x5 == 0x2e
XOR: 0x34 ^ 0xd7 = 0xe3
CMP: 0x6 == 0x2e
XOR: 0x37 ^ 0x84 = 0xb3
CMP: 0x7 == 0x2e
XOR: 0x36 ^ 0x3a = 0xc
CMP: 0x8 == 0x2e
XOR: 0x39 ^ 0xf5 = 0xcc
CMP: 0x9 == 0x2e
XOR: 0x38 ^ 0xc2 = 0xfa
CMP: 0xa == 0x2e
XOR: 0x3b ^ 0xc2 = 0xf9
CMP: 0xb == 0x2e
XOR: 0x3a ^ 0x22 = 0x18
CMP: 0xc == 0x2e
XOR: 0x3d ^ 0x48 = 0x75
CMP: 0xd == 0x2e
XOR: 0x3c ^ 0x1d = 0x21
CMP: 0xe == 0x2e
XOR: 0x3f ^ 0x14 = 0x2b
CMP: 0xf == 0x2e
XOR: 0x3e ^ 0x2a = 0x14
CMP: 0x10 == 0x2e
XOR: 0x21 ^ 0x71 = 0x50
CMP: 0x11 == 0x2e
XOR: 0x20 ^ 0x25 = 0x5
CMP: 0x12 == 0x2e
XOR: 0x23 ^ 0xa7 = 0x84
CMP: 0x13 == 0x2e
XOR: 0x22 ^ 0x73 = 0x51
CMP: 0x14 == 0x2e
XOR: 0x25 ^ 0x3c = 0x19
CMP: 0x15 == 0x2e
XOR: 0x24 ^ 0x9c = 0xb8
CMP: 0x16 == 0x2e
XOR: 0x27 ^ 0x72 = 0x55
CMP: 0x17 == 0x2e
XOR: 0x26 ^ 0xfe = 0xd8
CMP: 0x18 == 0x2e
XOR: 0x29 ^ 0x3c = 0x15
CMP: 0x19 == 0x2e
XOR: 0x28 ^ 0xb7 = 0x9f
CMP: 0x1a == 0x2e
XOR: 0x2b ^ 0xad = 0x86
CMP: 0x1b == 0x2e
XOR: 0x2a ^ 0x80 = 0xaa
CMP: 0x1c == 0x2e
XOR: 0x2d ^ 0xa9 = 0x84
CMP: 0x1d == 0x2e
XOR: 0x2c ^ 0x6f = 0x43
CMP: 0x1e == 0x2e
XOR: 0x2f ^ 0x37 = 0x18
CMP: 0x1f == 0x2e
XOR: 0x2e ^ 0x46 = 0x68
CMP: 0x20 == 0x2e
XOR: 0x11 ^ 0x91 = 0x80
CMP: 0x21 == 0x2e
XOR: 0x10 ^ 0x32 = 0x22
CMP: 0x22 == 0x2e
XOR: 0x13 ^ 0xb4 = 0xa7
CMP: 0x23 == 0x2e
XOR: 0x12 ^ 0xf7 = 0xe5
CMP: 0x24 == 0x2e
XOR: 0x15 ^ 0xa5 = 0xb0
CMP: 0x25 == 0x2e
XOR: 0x14 ^ 0xad = 0xb9
CMP: 0x26 == 0x2e
XOR: 0x17 ^ 0xd8 = 0xcf
CMP: 0x27 == 0x2e
XOR: 0x16 ^ 0x6b = 0x7d
CMP: 0x28 == 0x2e
XOR: 0x19 ^ 0x35 = 0x2c
CMP: 0x29 == 0x2e
XOR: 0x18 ^ 0x8c = 0x94
CMP: 0x2a == 0x2e
XOR: 0x1b ^ 0xe4 = 0xff
CMP: 0x2b == 0x2e
XOR: 0x1a ^ 0x0 = 0x1a
CMP: 0x2c == 0x2e
XOR: 0x1d ^ 0x20 = 0x3d
CMP: 0x2d == 0x2e
XOR: 0x1c ^ 0x2e = 0x32
CMP: 0x2e == 0x2e

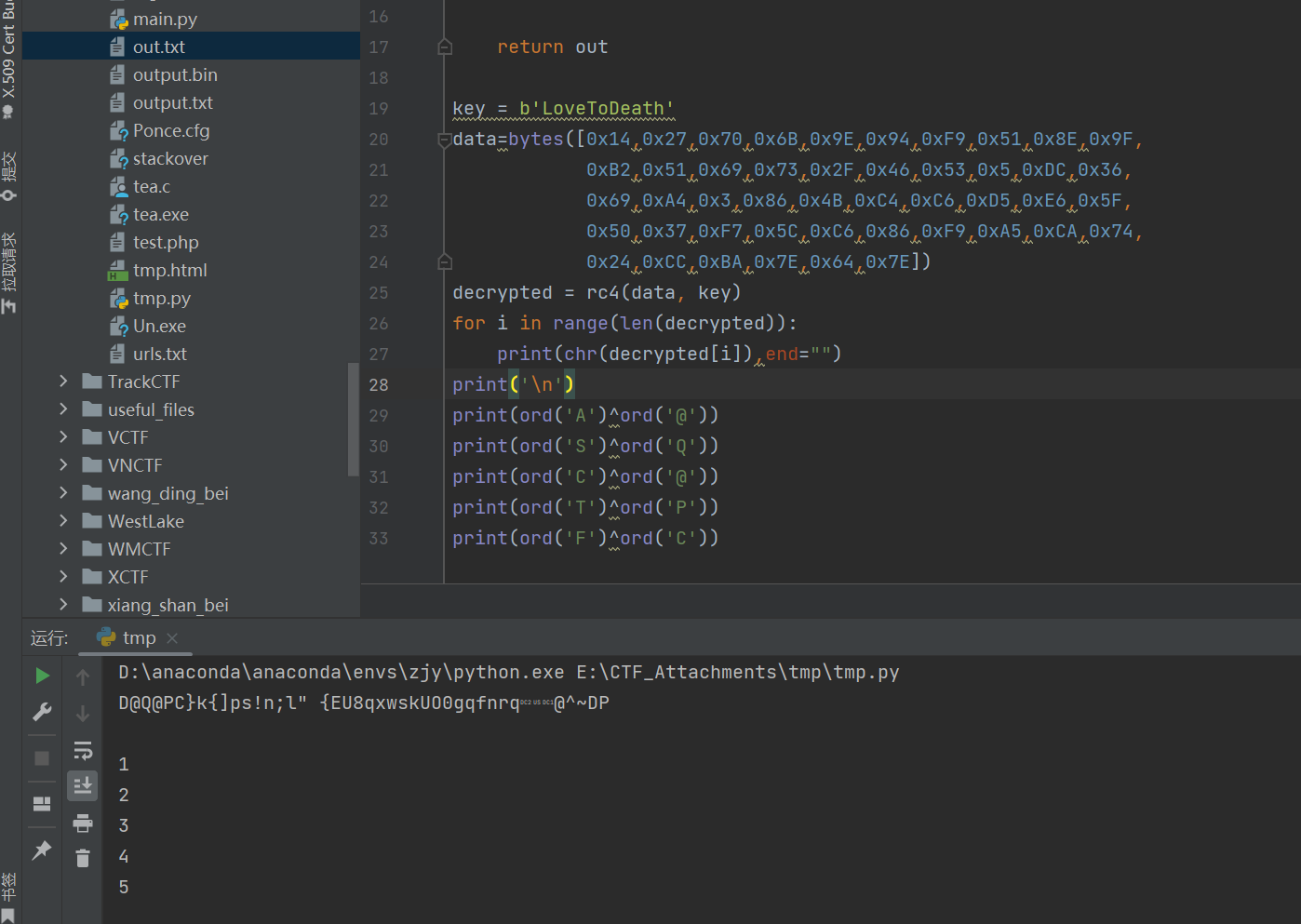
两次256轮循环猜测可能是rc4，第一步是把明文xor 下标，然后标准rc4加密

按照思路直接写脚本，发现逆向之后就是flag

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
key=[0x50, 0x67, 0x21, 0x2b, 0xce, 0xd7, 0x84, 0x3a, 0xf5, 0xc2,
     0xc2, 0x22, 0x48, 0x1d, 0x14, 0x2a, 0x71, 0x25, 0xa7, 0x73,
     0x3c, 0x9c, 0x72, 0xfe, 0x3c, 0xb7, 0xad, 0x80, 0xa9, 0x6f,
     0x37, 0x46, 0x91, 0x32, 0xb4, 0xf7, 0xa5, 0xad, 0xd8, 0x6b,
     0x35, 0x8c, 0xe4, 0x0, 0x20, 0x2e]

enc=[0x14,0x27,0x70,0x6B,0x9E,0x94,0xF9,0x51,0x8E,0x9F,
     0xB2,0x51,0x69,0x73,0x2F,0x46,0x53,0x5,0xDC,0x36,
     0x69,0xA4,0x3,0x86,0x4B,0xC4,0xC6,0xD5,0xE6,0x5F,
     0x50,0x37,0xF7,0x5C,0xC6,0x86,0xF9,0xA5,0xCA,0x74,
     0x24,0xCC,0xBA,0x7E,0x64,0x7E]

flag=''
for i in range(len(enc)):
    tmp=enc[i]^i^key[i]
    flag+=chr(tmp)
print(flag)
# DASCTF{lsTzx-c5c21iVA-goojqNS-ynFOPRx-489itUh}

正常做法应该写脚本模拟所有操作并trace或者一点点调试，这里小小猜测一手，算是非预期

下面脚本也可以验证加密流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def rc4(data, key):
    S = list(range(256))
    j = 0
    out = []

    for i in range(256):
        j = (j + S[i] + key[i % len(key)]) % 256
        S[i], S[j] = S[j], S[i]

    i = j = 0
    for char in data:
        i = (i + 1) % 256
        j = (j + S[i]) % 256
        S[i], S[j] = S[j], S[i]
        out.append(char ^ S[(S[i] + S[j]) % 256])

    return out

key = b'LoveToDeath'
data=bytes([0x14,0x27,0x70,0x6B,0x9E,0x94,0xF9,0x51,0x8E,0x9F,
            0xB2,0x51,0x69,0x73,0x2F,0x46,0x53,0x5,0xDC,0x36,
            0x69,0xA4,0x3,0x86,0x4B,0xC4,0xC6,0xD5,0xE6,0x5F,
            0x50,0x37,0xF7,0x5C,0xC6,0x86,0xF9,0xA5,0xCA,0x74,
            0x24,0xCC,0xBA,0x7E,0x64,0x7E])
decrypted = rc4(data, key)
flag=''
for i in range(len(decrypted)):
    decrypted[i]^=i
    flag+=chr(decrypted[i])
print(flag)
#DASCTF{lsTzx-c5c21iVA-goojqNS-ynFOPRx-489itUh}

既然这样的话我知道大部分人怎么做出来的了，这题看到key和密文长度46，猜一手rc4，然后观察解密后的数据和格式发现还需要异或i直接出，可见CTF解题还是需要一些“巧劲”

信创安全

X1-1

两次解包hap文件得到moudles.abc文件，反编译后找到Index类，发现关键加密

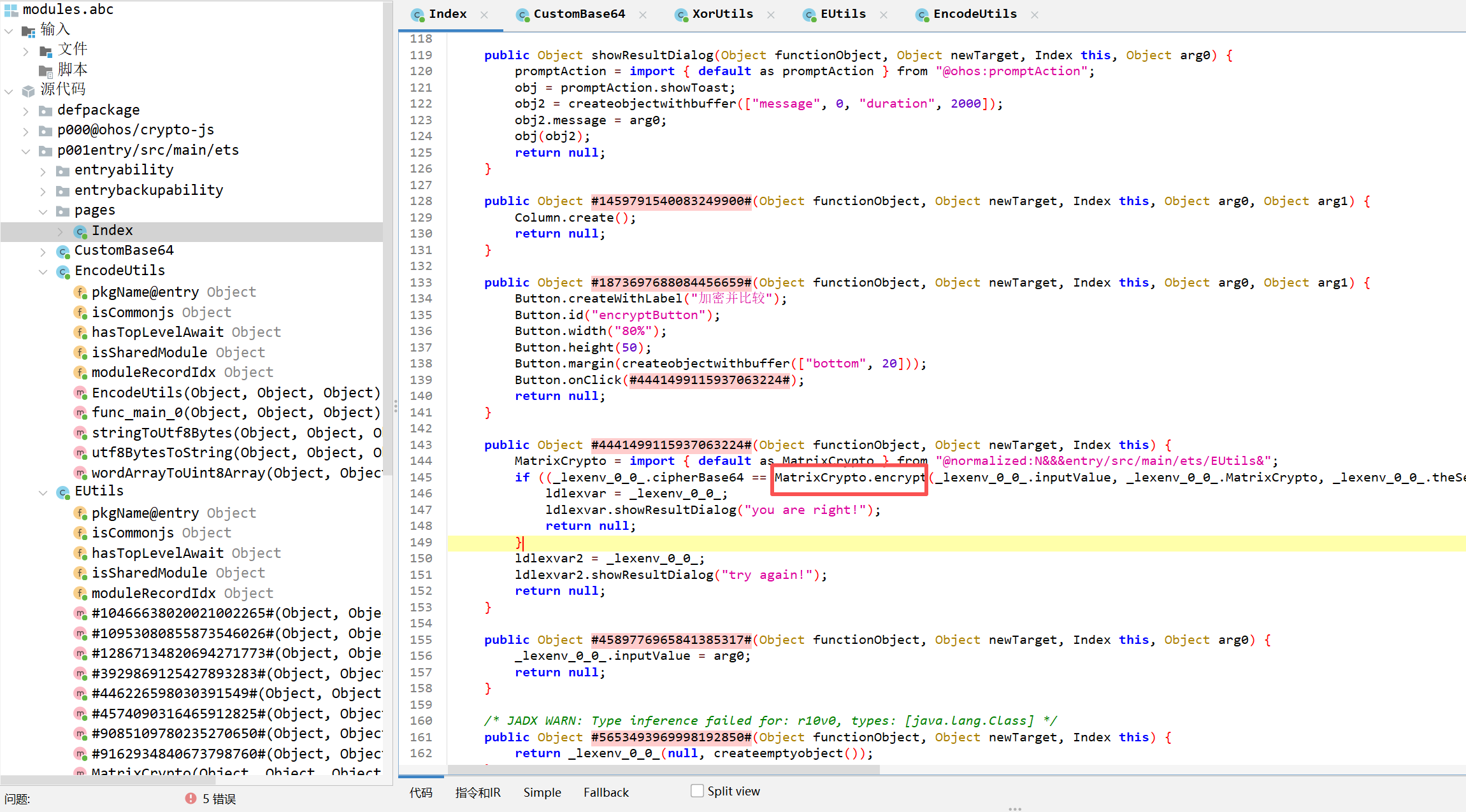
arg0是input，arg1是3*3矩阵，arg2是theSecondKey，arg3是arc4Key

分别进行矩阵加密（输入和arg1），异或，rc4，自定义码表的 base64

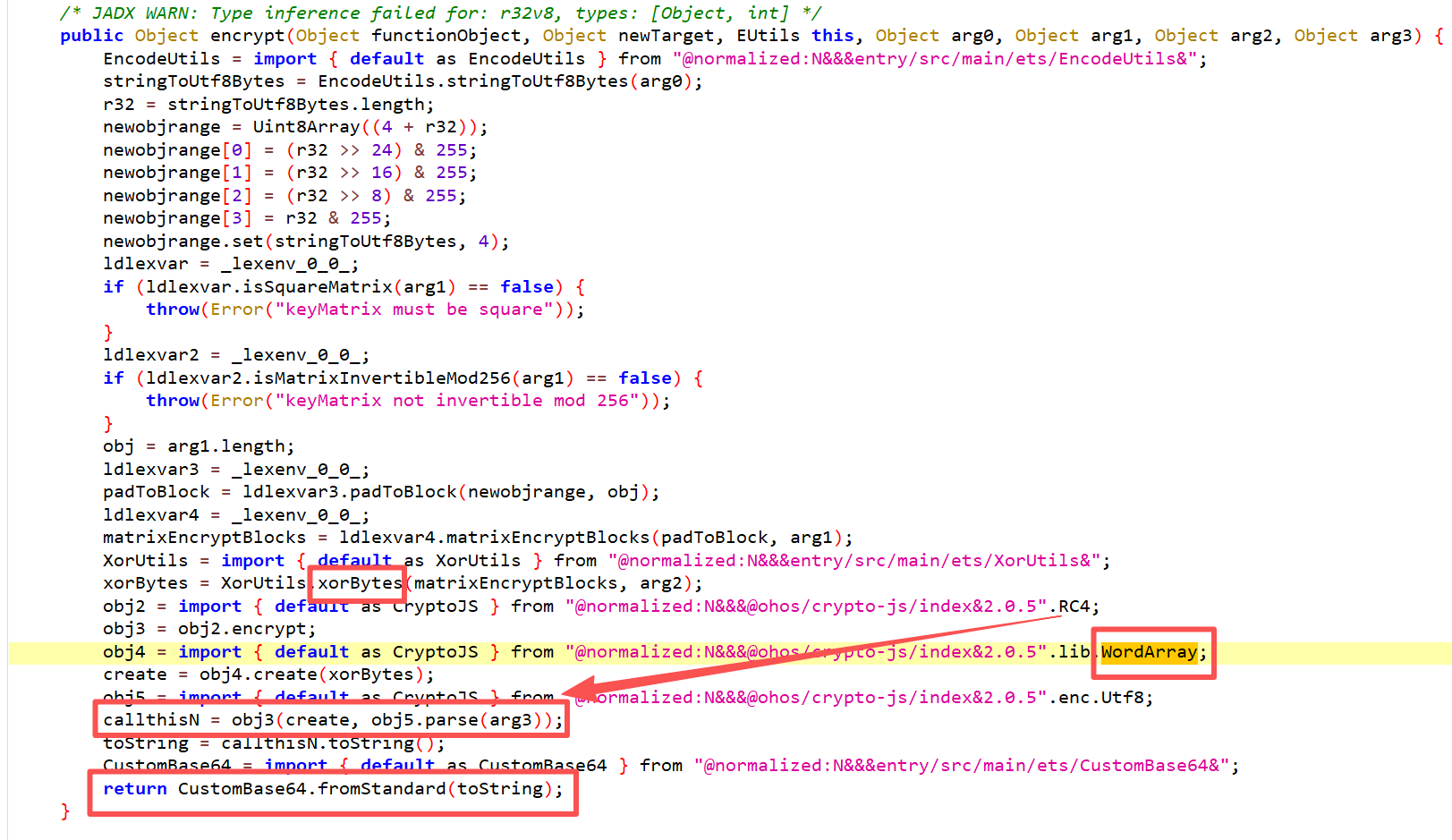
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
import base64
from Crypto.Cipher import ARC4
import numpy as np

cipher = "37L9UF8uNl1TSgYMLIW/RosGPMxVYXNcUoTTQXihX8ZyaQVgxY9Ywz/0fIwRzI4H"
key2 = bytes([90, 60, 231, 145, 47])
rc4_key = b"HarMonyOS_S3cur3_K3y!2025"

custom_b64 = "3GHIJKLMzxy01245PQRSTUFabcdefghijklmnopqrstuv6789+/NOVWXYZABCDEw"
std_b64 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
translate_table = str.maketrans(custom_b64, std_b64)


def custom_b64_decode(s):
    std_s = s.translate(translate_table)
    return base64.b64decode(std_s)

def rc4_decrypt(data, key):
    cipher = ARC4.new(key)
    return cipher.decrypt(data)

def xor_decrypt(data, key):
    result = bytearray()
    for i, byte in enumerate(data):
        result.append(byte ^ key[i % len(key)])
    return bytes(result)


def extended_gcd(a, b):
    """扩展欧几里得算法，返回 (gcd, x, y) 使得 ax + by = gcd(a, b)"""
    if a == 0:
        return b, 0, 1
    gcd, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return gcd, x, y


def mod_inverse(a, m):
    """计算 a 在模 m 下的逆元"""
    gcd, x, _ = extended_gcd(a, m)
    if gcd != 1:
        raise ValueError(f"{a} 在模 {m} 下没有逆元")
    return x % m


def matrix_inverse_mod(matrix, mod=256):
    """计算矩阵在模 mod 下的逆矩阵（使用伴随矩阵法）"""
    n = len(matrix)

    # 计算行列式（模 mod）
    det = int(np.round(np.linalg.det(matrix))) % mod
    if det == 0:
        raise ValueError("矩阵行列式为0，不可逆")

    # 计算行列式的模逆
    det_inv = mod_inverse(det, mod)

    # 计算伴随矩阵
    adj = np.zeros((n, n), dtype=int)

    for i in range(n):
        for j in range(n):
            # 计算代数余子式
            # 删除第i行第j列
            minor = np.delete(np.delete(matrix, i, axis=0), j, axis=1)
            # 计算余子式
            cofactor = (-1) ** (i + j) * int(np.round(np.linalg.det(minor)))
            # 伴随矩阵是代数余子式矩阵的转置
            adj[j][i] = cofactor % mod

    # 计算逆矩阵：伴随矩阵 × 行列式逆元 (模 mod)
    inv_matrix = (adj * det_inv) % mod
    return inv_matrix

def matrix_decrypt(data):
    M = [[1, 2, 3],
         [0, 1, 4],
         [0, 0, 1]]

    inv_M = matrix_inverse_mod(M, 256)

    decrypted = bytearray()
    for i in range(0, len(data), 3):
        block = data[i:i + 3]

        # 矩阵乘法：P = M^{-1} * C (mod 256)
        x, y, z = block
        x_dec = (inv_M[0][0] * x + inv_M[0][1] * y + inv_M[0][2] * z) % 256
        y_dec = (inv_M[1][0] * x + inv_M[1][1] * y + inv_M[1][2] * z) % 256
        z_dec = (inv_M[2][0] * x + inv_M[2][1] * y + inv_M[2][2] * z) % 256
        decrypted.extend([x_dec, y_dec, z_dec])

    return bytes(decrypted)


step1 = custom_b64_decode(cipher)
step2 = rc4_decrypt(step1, rc4_key)
step3 = xor_decrypt(step2, key2)
step4 = matrix_decrypt(step3)
print("flag:",step4)
#DASCTF{H4rmOny0S_Mult1_L4y3r_Crypt0_M4st3r!}

也可以先base64和rc4解密

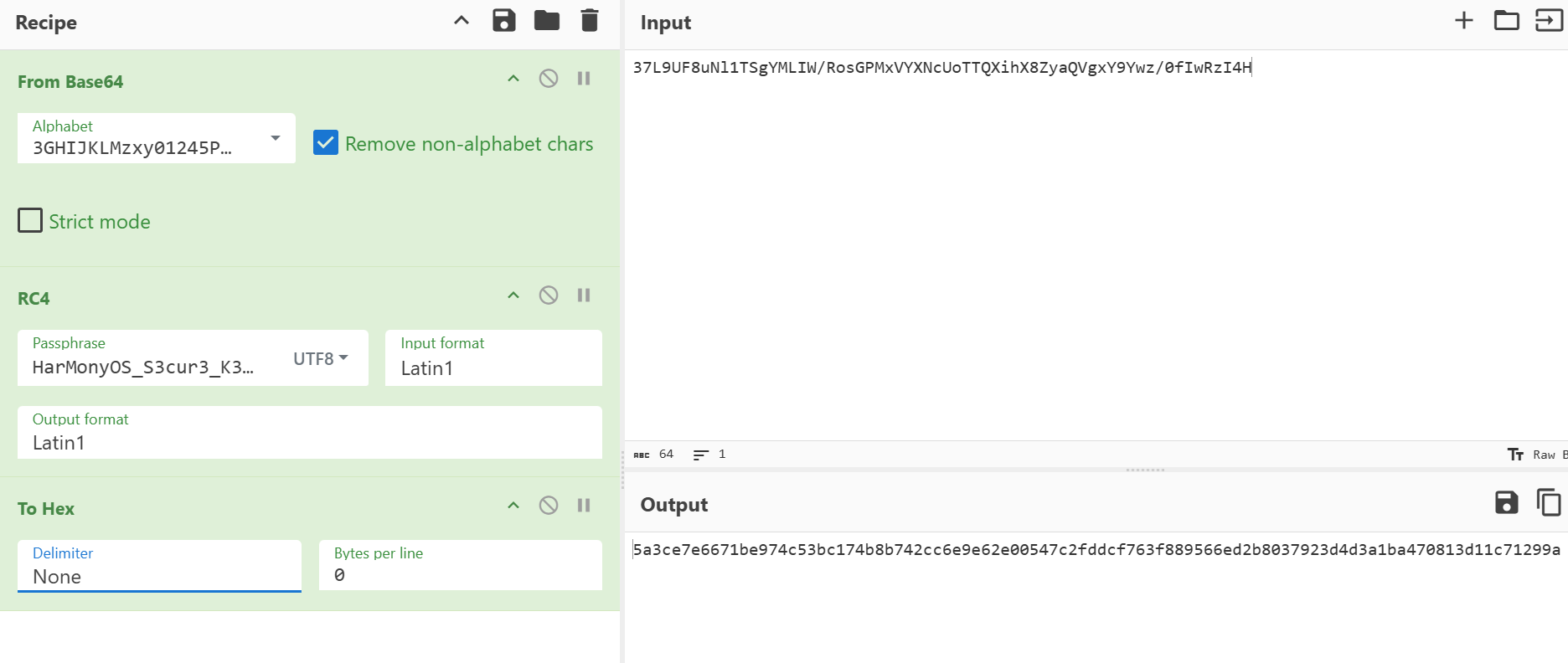
再进行矩阵运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import binascii
from sympy import Matrix

A = [
    [1, 2, 3],
    [0, 1, 4],
    [0, 0, 1],
]

out = bytearray(binascii.unhexlify("5a3ce7e6671be974c53bc174b8b742cc6e9e62e00547c2fddcf763f889566ed2b8037923d4d3a1ba470813d11c71299a"))

xor_key = [90, 60, 231, 145, 47]

for i in range(len(out)):
    out[i] ^= xor_key[i % len(xor_key)]

n = len(A)

cipther = np.frombuffer(bytes(out), dtype=np.uint8)

inv = Matrix(np.array(A, dtype=int)).inv_mod(256)

out = bytearray()
for block in cipther.reshape(-1, n):#-1 表示自动计算行数
    plain = (inv @ block) % 256
    out.extend(plain.astype(np.uint8))

print(out)

整体逻辑很清晰，就是比赛期间写不出矩阵相关代码🤔

比赛wp
#VM #base32 #矩阵
浙江省省赛2025决赛wp
https://j1ya-22.github.io/2025/11/16/浙江省省赛2025决赛wp/
作者
j1ya
发布于
2025年11月16日
许可协议